判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
1、设函数 ,且f(u)二阶可导,则
,且f(u)二阶可导,则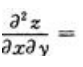 ().
().
- A:
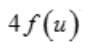
- B:
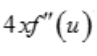
- C:
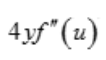
- D:
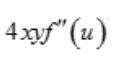
答 案:D
解 析: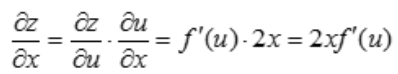 ,
,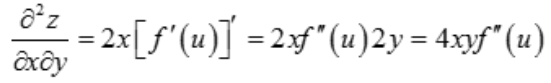 .
.
2、设函数f(x)在(∞,+∞)上可导,且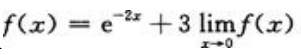 则f'(x)等于().
则f'(x)等于().
- A:
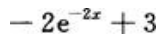
- B:
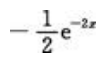
- C:
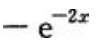
- D:
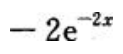
答 案:D
解 析:函数f(x)在(-∞,+∞)上可导,故函数在(-∞,+∞)连续, 为常数,设
为常数,设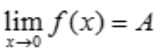 ,故
,故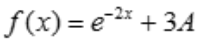 ,
, .
.
主观题
1、求函数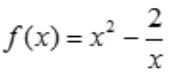 的单调区间、极值、凹凸区间和拐点.
的单调区间、极值、凹凸区间和拐点.
答 案:解:f(x)的定义域为(-∞,0)∪(0,+∞),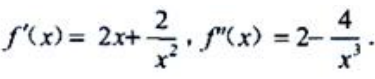 令
令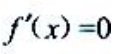 ,得x=-1.令
,得x=-1.令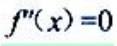 ,得
,得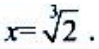
列表得
所以函数f(x)的单调减少区间为(-∞,-1),单调增加区间(-1,0),(0,+∞);
f(-1)=3为极小值,无极大值.
函数f(x)的凹区间为(-∞,0),(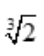 ,+∞),凸区间为(0,
,+∞),凸区间为(0,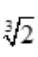 ),拐点坐标为(
),拐点坐标为(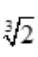 ,0).
,0).
2、每次抛掷一枚骰子(6个面上分别标有数字1、2、3、4、5、6),连续抛掷2次,设A={向上的数字之和为6},求P(A).
答 案:解:基本事件数为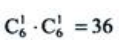 抛掷两次,向上的数字之和为6的事件共有5种,即(1,5),(2,4),(3,3),(4,2),(5,1).注意事件(1,5)与(5,1)是两个不同的事件:第一次出现1或5而第二次出现5或1是两个不同的结果,所以P(A)=
抛掷两次,向上的数字之和为6的事件共有5种,即(1,5),(2,4),(3,3),(4,2),(5,1).注意事件(1,5)与(5,1)是两个不同的事件:第一次出现1或5而第二次出现5或1是两个不同的结果,所以P(A)= .
.
填空题
1、函数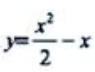 的单调增加区间是().
的单调增加区间是().
答 案:(1,+∞)
解 析: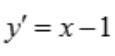 ,当y'>0,即x>1时,函数单调增加,故函数的单调增加区间为(1,+∞).
,当y'>0,即x>1时,函数单调增加,故函数的单调增加区间为(1,+∞).
2、 =().
=().
答 案:xcosx-sinx+C
解 析:由分部积分得
简答题
1、已知函数f(x)=ax3-bx2+cx在区间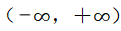 内是奇函数,且当x=1时,f(x)有极小值
内是奇函数,且当x=1时,f(x)有极小值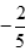 ,求另一个极值及此曲线的拐点.
,求另一个极值及此曲线的拐点.
答 案:f(x)=ax3-bx2+cx,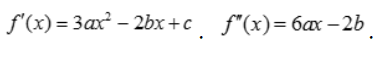 由于f(x)是奇函数,则必有x2的系数为0,即b=0.
由于f(x)是奇函数,则必有x2的系数为0,即b=0.
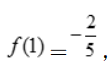 即a+c=
即a+c=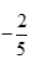 ,
,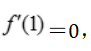 得3a+c=0.解得a=
得3a+c=0.解得a=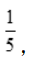 c=
c= 此时
此时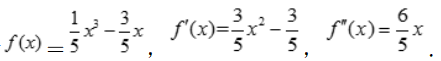 令
令 得
得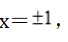
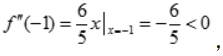 所以
所以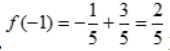 为极大值,
为极大值,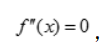 得x=0,x<0时,
得x=0,x<0时,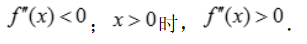 所以(0,0)为曲线的拐点.
所以(0,0)为曲线的拐点.
2、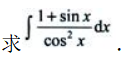
答 案:

