2024年成考专升本《高等数学一》每日一练试题07月10日
考试问答
2024-07-10
11:30:11
收藏
单选题
1、函数y=f(x)在点x0处可导的充分必要条件是()。
- A:它在该点处的左导数和右导数存在
- B:它在该点处连续
- C:它在该点处存在极限
- D:它在该点处可微
答 案:D
解 析:D项,对于一元函数来说,函数在某一点可导和在某一点可微等价.A项,函数在某一点的左导数和右导数存在且相等是函数在该点可导的充分必要条件.B项,可导一定连续,但连续不一定可导,例如函数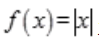 在x=0连续但不可导;C项,极限存在与函数存在不存在必然联系。
在x=0连续但不可导;C项,极限存在与函数存在不存在必然联系。
2、微分方程y''=3x的通解是()。
- A:
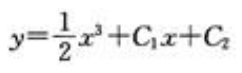
- B:
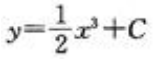
- C:
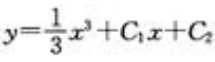
- D:
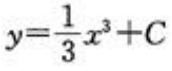
答 案:A
解 析:y''=3x,则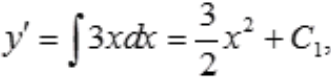
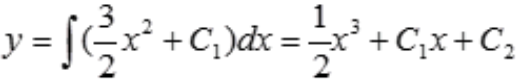 。
。
3、设z=2x2+3xy-y2,则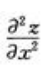 等于()。
等于()。
- A:4
- B:3
- C:2
- D:-2
答 案:A
解 析: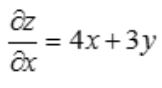 ,
,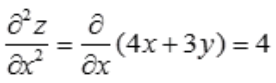 。
。
主观题
1、求微分方程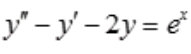 的通解。
的通解。
答 案:解:对应的齐次方程为 。特征方程
。特征方程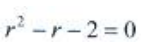 ,特征根
,特征根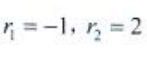 齐次方程通解为
齐次方程通解为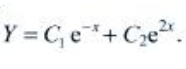 原方程特解为
原方程特解为 ,代入原方程可得
,代入原方程可得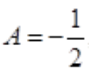 ,因此
,因此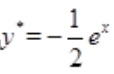 。
。
方程通解为
2、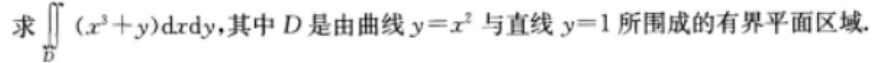
答 案:
3、将f(x)=sin3x展开为x的幂级数,并指出其收敛区间。
答 案:解:由于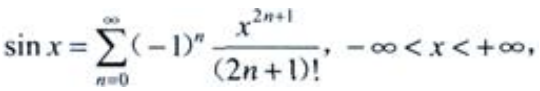 可知
可知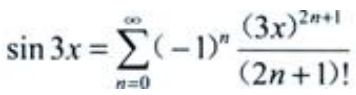
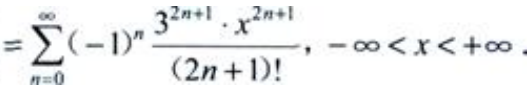
填空题
1、微分方程y'=ex-y满足初始条件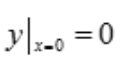 的特解是()。
的特解是()。
答 案:y=x
解 析:对微分方程分离变量得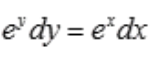 ,等式两边同时积分得
,等式两边同时积分得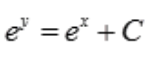 ,将x=0,y=0代入得C=0,故微分方程的特解为y=x。
,将x=0,y=0代入得C=0,故微分方程的特解为y=x。
2、过点M0(1,-2,0)且与直线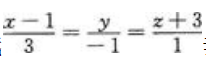 垂直的平面方程为()。
垂直的平面方程为()。
答 案:3(x-1)-(y+2)+x=0(或3x-y+z=5)
解 析:因为直线的方向向量s=(3,-1,1),且平面与直线垂直,所以平面的法向量 ,由点法式方程有平面方程为:3(x-1)-(y+2)+(z-0)=0,即3(x-1)-(y+2)+z=0。
,由点法式方程有平面方程为:3(x-1)-(y+2)+(z-0)=0,即3(x-1)-(y+2)+z=0。
3、若f(x)是连续函数的偶函数,且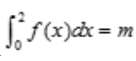 ,则
,则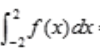 =()。
=()。
答 案:2m
解 析:由于f(x)为连续的偶函数,因此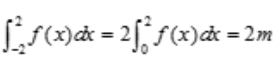 。
。
简答题
1、计算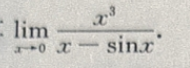
答 案: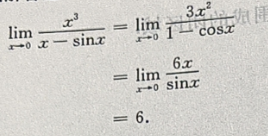
更多推荐

