2024年成考专升本《高等数学二》每日一练试题07月05日
考试问答
2024-07-05
11:24:31
收藏
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
1、直线l与x轴平行,且与曲线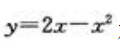 相切,则切点的坐标是().
相切,则切点的坐标是().
- A:(1,1)
- B:(-1,1)
- C:(0,-1)
- D:(0,1)
答 案:A
解 析:曲线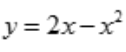 的切线斜率为
的切线斜率为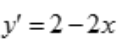 ,又切线l与x轴平行,则
,又切线l与x轴平行,则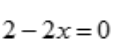 ,得切点横坐标x=1,带入曲线
,得切点横坐标x=1,带入曲线 得纵坐标y=1,所以切点坐标是(1,1).
得纵坐标y=1,所以切点坐标是(1,1).
2、函数f(x)=2x3-9x2+3的单调递减区间是()。
- A:(3,+∞)
- B:(-∞,+∞)
- C:(-∞,0)
- D:(0,3)
答 案:D
解 析:本题考查了单调区间的知识点 由题可得f’(x)=6x2+18x=6x(x-3),令f’(x)<0,得0<x<3,故单调减区间为(0,3)。
主观题
1、设事件A与B相互独立,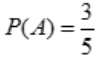 ,
,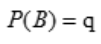 ,
,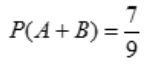 ,求q.
,求q.
答 案:解:因为事件A与B相互独立,故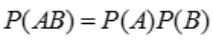 ,
, ,即
,即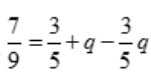 ,解得
,解得 =
=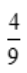 .
.
2、在15件产品中,有2件是次品,另外13件是正品.现从中任取3件产品.求取出的3件产品中:(1)恰有1件是次品的概率;
(2)至少有1件次品的概率.
答 案:解:(1)P(恰有1件次品)=
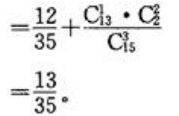 (2)P(至少有1件次品)=P(恰有1件次品)+P(恰有2件次品)
(2)P(至少有1件次品)=P(恰有1件次品)+P(恰有2件次品)
填空题
1、函数y=ln(arcsinx)的连续区间为().
答 案:(0,1]
解 析:函数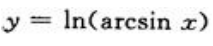 的连续区间为它的定义区间,由
的连续区间为它的定义区间,由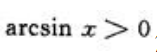 解得x∈(0,1].
解得x∈(0,1].
2、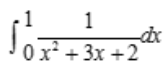 =().
=().
答 案: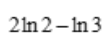
解 析: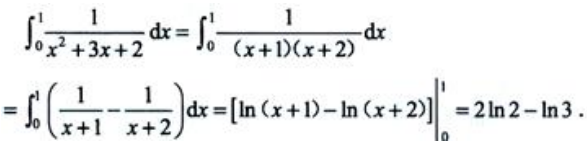
简答题
1、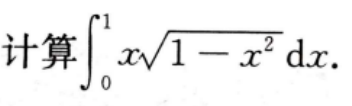
答 案: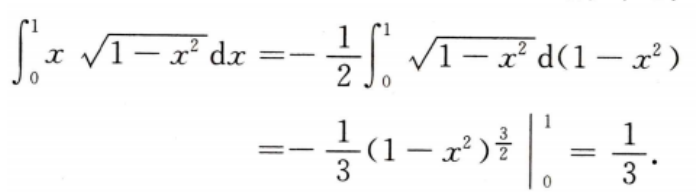
2、计算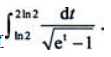
答 案: 设
设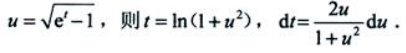 则
则
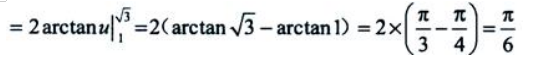
更多推荐

