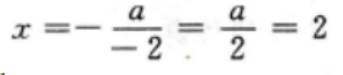单选题

1、已知集合M =(2,3,5,a),N =(1,3,4,b),若M∩N=(1,2,3),则a,b的值为  

• A：a=2,b=1
• B：a=1,b=1
• C：a=1,b= 2
• D：a=1,b=5

答 案：C

解 析：M∩N={2,3,5,a} ∩{1,3,4,6} ={1,2,3} 又因为M中无“1”元素，而有“a”元素，只有a=1 而N中无“2”元素，而有“b元素”，只有b=2  

2、设双曲线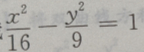的渐近线的斜率为k，则|k|=（）  

• A：
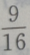
• B：
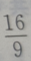
• C：
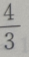
• D：

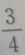
答 案：D

解 析：双曲线渐近线的斜率为k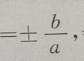故本题中k

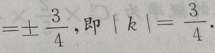
3、函数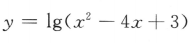的定义域是（）

• A：{x|-3＜x＜-1}
• B：{x|x＜-3或x＞-1}
• C：{x|1＜x＜3}
• D：{x|x＜1或x＞3}

答 案：D

解 析：由对数函数的性质可知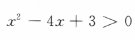，解得x＞3或x＜1，因此函数的定义域为{x|x＜1或x＞3}

4、若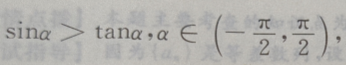则（）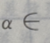

• A：
• B：
• C：
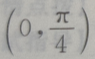
• D：

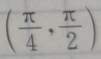
答 案：B

解 析：首先做出单位圆,然后根据问题的约束条件,利用三角函数线找出满足条件的a角取值范围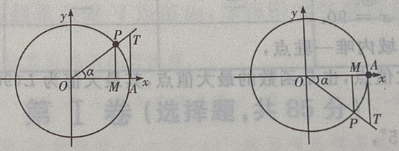  

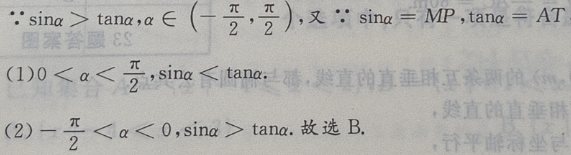
主观题

1、已知直线l的斜率为1，l过抛物线C：的焦点，且与C交于A,B两点.(I）求l与C的准线的交点坐标；
(II）求|AB|.

答 案：(I）C的焦点为，准线为由题意得l的方程为因此l与C的准线的交点坐标为(II）由，得设A（x1,y1），B（x2,y2），则因此

2、在△ABC中，B=120°,BC=4,△ABC的面积为，求AC.

答 案：由△ABC的面积为得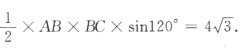所以AB =4.因此所以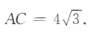

3、已知函数f(x)=(x-4)(x²-a) （I）求f"(x)； (Ⅱ)若f"(-1)=8，求f(x)在区间[0，4]的最大值与最小值

答 案：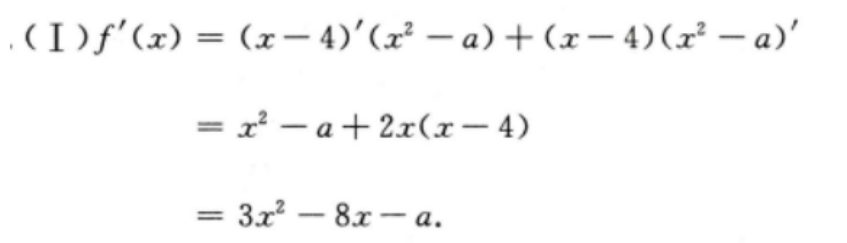

4、已知等差数列｛an｝中，a1+a2+a3=6,a2+a4+a5= 12求｛an｝的首项与公差。  

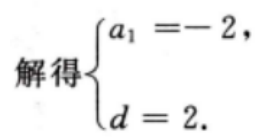
答 案：因为｛an｝为等差数列，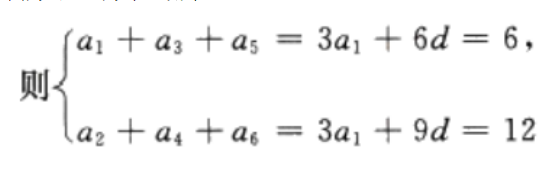

填空题

1、函数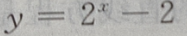的图像与坐标轴的交点共有（）  

答 案：2

解 析：当x=0时，y=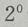-2=-1，故函数与y轴交于(0,-1)点，令y=0,则有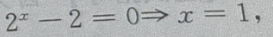故函数与x轴交于(1,0) 点,因此函数 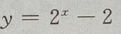与坐标轴的交点共有 2个.

2、函数y=-x²+ax图像的对称轴为x=2，则a=______。  

答 案：4

解 析：本题主要考查的知识点为二次函数的性质 由题意，该函数图像的对称轴为