单选题
1、设y＝e2x，则dy＝（）。
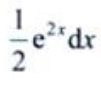
答 案：B
解 析：由复合函数的求导法则可知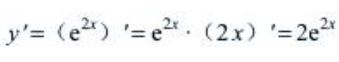
，故
。
2、设z=(y-x)2+
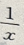，则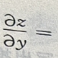
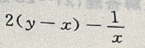
答 案：D
解 析：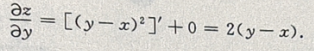
3、微分方程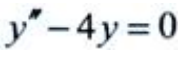
的特征根为（）。
答 案：B
解 析：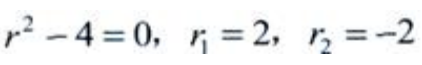
。
主观题
1、求曲线y＝x2在点（a，a2）（a＜1）的一条切线，使由该切线与x＝0、x＝1和y＝x2所围图形的面积最小。
答 案：解：设所求切线的切点为（a，b），见下图，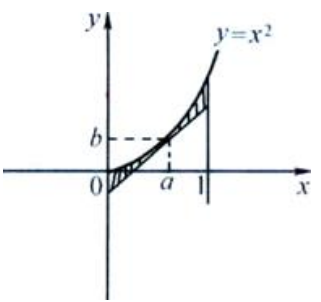
则b＝a2，
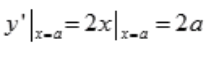，切线方程为y－b＝2a（x－a），y＝2ax－2a2＋b＝2ax－a2。设对应图形面积为A，则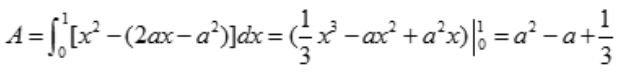
令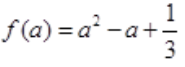
，则
，令
。当a＜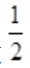
时，f'(a)＜0；当a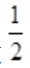＞时，f'(a)＞0，故
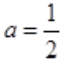为f(a)的最小值点，切线方程为：y＝x－
。
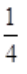2、设D是由直线y＝x与曲线y＝x3在第一象限所围成的图形.（1）求D的面积S；
（2）求D绕x轴旋转一周所得旋转体的体积V。
答 案：解：由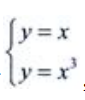
，知两曲线的交点为（0，0），（1，1）和（-1，-1），则（1）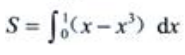
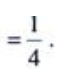（2）
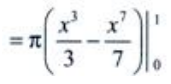
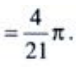
3、求y＝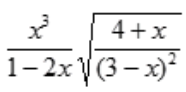
的一阶导数y'。
答 案：解：两边取对数得
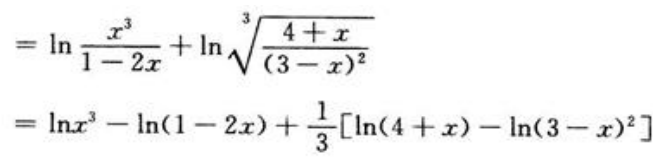两边对x求导得
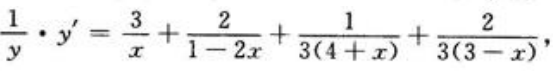故
填空题
1、设区域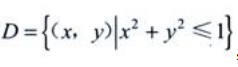
，则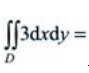
（）。
答 案：3π
解 析：积分区域D为半径为1的圆域，其面积为π，因此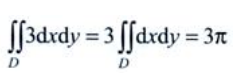
。
2、设I=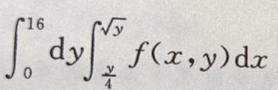
交换积分次序，则有I=（）
答 案：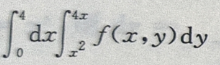
解 析：
的积分区域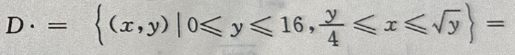
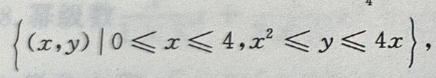
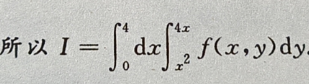
3、幂级数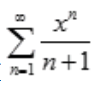
的收敛半径是（）。
答 案：1
解 析：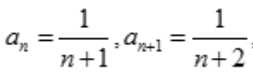
，
。
简答题
1、求微分方程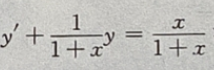
满足初值条件
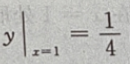的特解
答 案：
