判断题

1、{x|x²=-1，x∈R}是空集。（）  

答 案：对

解 析：x^2恒大于0，则x^2=-1无解。所以该集合没有元素，为空集。故正确

2、函数y=1/x在(0,+∞)上单调递减。（）  

答 案：对

单选题

1、已知双曲线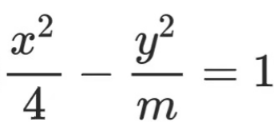的离心率为2，则实数m=_______  

• A：10
• B：12
• C：14
• D：16

答 案：B

2、x=0是xy=0的()  

• A：充分非必要条件
• B：必要非充分条件
• C：充要条件
• D：既不充分也不必要条件

答 案：A

解 析：当x=0时，则xy=0，即充分性成立；当xy=0时，则x=0或者y=0，即必要性不成立；即x=0是xy=0的充分不必要条件

多选题

1、下列计算结果正确的是（）  

• A：
• B：
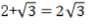
• C：
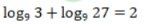
• D：

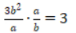
答 案：AC

2、已知向量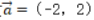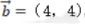，，则（）  

• A：
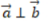
• B：
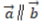
• C：
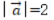
• D：

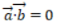
答 案：AD

解 析：若设a=(x1,y1)，b=(x2,y2)，a⊥b的充要条件是a·b=0，即(x1x2+y1y2)=0。本题中-2*4+2*4=0，则两个向量垂直

主观题

1、已知等差数列{an}的前n项和S_n且S₅=35,S₈=104.
(1)求数列{an}的通项公式；
(2)若{b_n}为等比数列，b₁=a₂,b₂=a₃+2,求数列{b,}的公比q及前n项和T_n.

答 案：(1)所以a₆=19.则数列{an}的公差，通项公式为an=a₆+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以则

2、已知函数f(x)=log₃(3x—1).(1)求函数f(x)的定义域；
(2)若f(x)<1,求x的取值范围.

答 案：(1)根据题意可得，3x-1>0,解得所以函数f(x)的定义域是(2)因为f(x)=log₃(3x-1)<1=log₃3,f(x)为定义域上的增函数，所以O<3x-1<3,解得所以x的取值范围是

填空题

1、不等式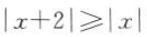的解集是（）.

答 案：[-1,+∞)

解 析：解不等式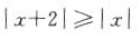,两边平方，移项整理得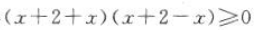,即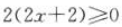,解得x≥-1,所以不等式的解集是[-1,+∞).

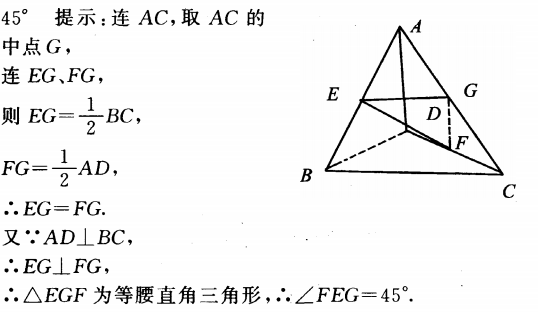
2、在空间四边形ABCD中，E、F分别是AB、CD的中点，AD丄BC，AD=BC，则EF和BC所成的角是_____.

答 案：45°

解 析：