2024年成考专升本《高等数学一》每日一练试题06月17日
考试问答
2024-06-17
11:26:59
收藏
单选题
1、微分方程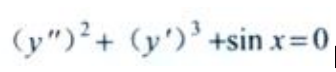 的阶数为()。
的阶数为()。
- A:1
- B:2
- C:3
- D:4
答 案:B
解 析:所给方程含有未知函数y的最高阶导数是2阶,因此方程的阶数为2。
2、如果级数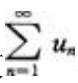 收敛,那么以下级数收敛的是()。
收敛,那么以下级数收敛的是()。
- A:
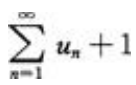
- B:
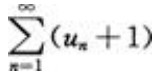
- C:
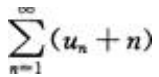
- D:
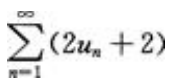
答 案:A
解 析:A项。级数 收敛,则
收敛,则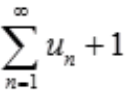 收敛;由极限收敛的必要条件可知,
收敛;由极限收敛的必要条件可知,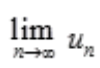 =0,则B项,
=0,则B项,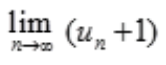 =1;C项,
=1;C项,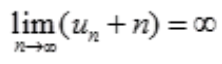 ;D项,
;D项,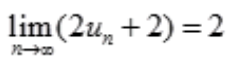 。
。
3、设y=x+lnx,dy=()。
- A:
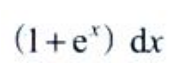
- B:
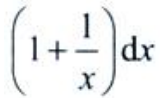
- C:
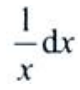
- D:
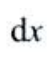
答 案:B
解 析:y=x+lnx,则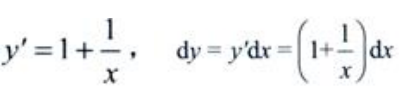 。
。
主观题
1、设f(x,y)为连续函数,交换二次积分 的积分次序。
的积分次序。
答 案:解:由题设知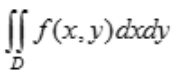 中积分区域的图形应满足1≤x≤e,0≤y≤lnx,因此积分区域的图形见下图中阴影部分
中积分区域的图形应满足1≤x≤e,0≤y≤lnx,因此积分区域的图形见下图中阴影部分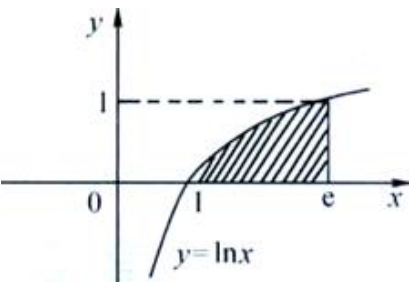 .由y=lnx,有x=ey。所以
.由y=lnx,有x=ey。所以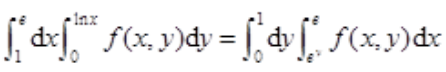 。
。
2、求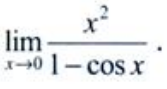
答 案:解:方法一:(洛必达法则)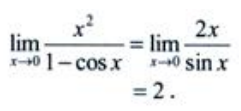 方法二:(等价无穷小)
方法二:(等价无穷小)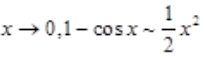
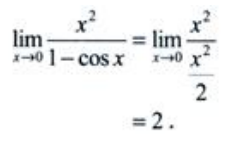
3、求函数y=xex的极小值点与极小值
答 案:解:方法一: 令y'=0,得x=-1。
令y'=0,得x=-1。
当x<-1时,y'<0;当x>-1时,y'>0。
故极小值点为x=-1,极小值为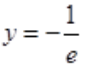 。
。
方法二:,
令y'=0,得x=-1,又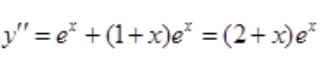 ,
, 。
。
故极小值点为x=-1,极小值为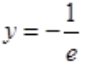 。
。
填空题
1、交换二次积分的积分次序,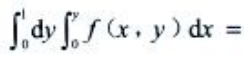 ()。
()。
答 案:
解 析:由题设有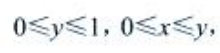 从而
从而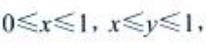 故交换次序后二次积分为
故交换次序后二次积分为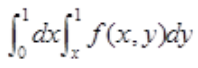 。
。
2、设z=arctanxy,则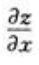 +
+ =()。
=()。
答 案: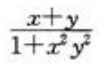
解 析: ,故
,故 。
。
3、过点M0(1,-1,0)且与平面x-y+3z=1平行的平面方程为=()。
答 案:x-y+3z=2
解 析:已知平面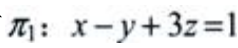 的法向量n1=(1,-1,3),所求平面π与π1平行,则平面π的法向量n//n1,取n=(1,-1,3),所求平面过点M0=(1,-1,0),由平面的点法式方程可知所求平面方程为
的法向量n1=(1,-1,3),所求平面π与π1平行,则平面π的法向量n//n1,取n=(1,-1,3),所求平面过点M0=(1,-1,0),由平面的点法式方程可知所求平面方程为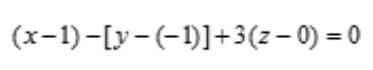 ,即x-y+3z=2。
,即x-y+3z=2。
简答题
1、已知函数f(x)连续,且满足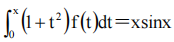 ,求f(x).
,求f(x).
答 案:由于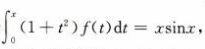 两边同时求导得
两边同时求导得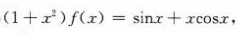 所以
所以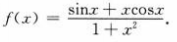
更多推荐

