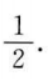单选题

1、设集合 （）。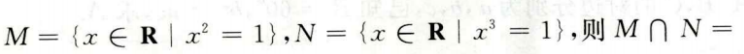

• A：{1}
• B：{-1}
• C：{—1，1）
• D：

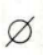
答 案：A

解 析：本题主要考查的知识点为集合的运算。 由题意M={-1，1}，N={1}，所以M∩N=（1}。  

2、在△ABC中，三边为a、b、c，∠B=60°，则的值是（）  

• A：大于零
• B：小于零
• C：等于零
• D：不能确定

答 案：C

解 析：由已知用余弦定理得：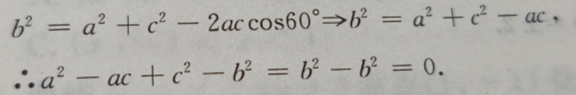  

3、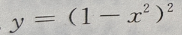的导数是  

• A：
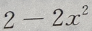
• B：
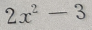
• C：
• D：

答 案：C

解 析：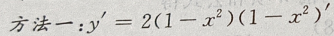

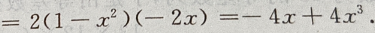
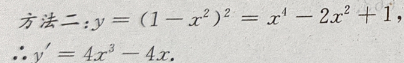
4、已知双曲线上一点到两焦点(-5,0),(5,0)距离之差的绝对值等于6,则双曲线方程为（）  

• A：
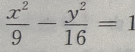
• B：
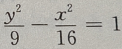
• C：
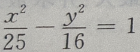
• D：

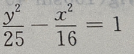
答 案：A

解 析：由已知条件知双曲线焦点在x轴上属于第一类标准式,又知c=5,2a=6, ∴a=3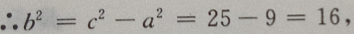，∴所求双曲线的方程为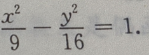  

主观题

1、在△ABC中,已知三边 a、b、c 成等差数列,且最大角∠A是最小角的2倍, a: b :c.  

答 案：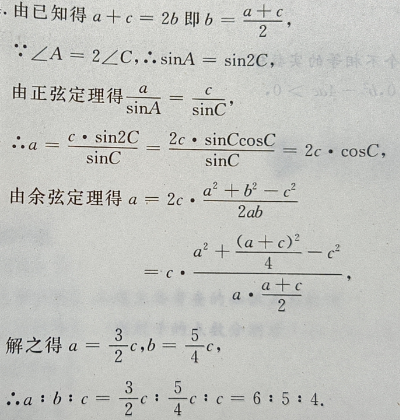

2、在△ABC中，AB=2，BC=3,B=60°，求AC及△ABC的面积

答 案：

3、已知三角形的一个内角是，面积是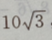周长是20,求各边的长.  

答 案：设三角形三边分别为a,b,c,∠A=60°，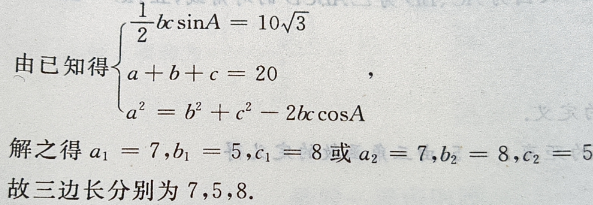  

4、已知抛物线C：y2=2px（p>0）的焦点到准线的距离为1。（I）求C的方程；
（Ⅱ）若A（1，m）（m>0）为C上一点，O为坐标原点，求C上另一点B的坐标，使得OA⊥OB。

答 案：(I)由题意,该抛物线的焦点到准线的距离为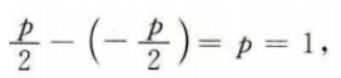 所以抛物线C的方程为y²=2x. (Ⅱ)因A(l,m)(m>0)为C上一点,故有m²=2, 可得 m=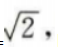因此A点坐标为 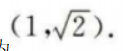设B点坐标为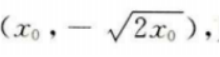

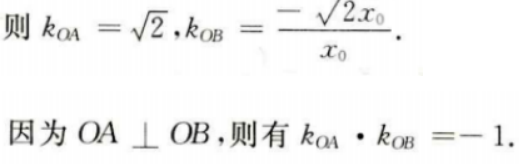
填空题

1、函数y=-x²+ax图像的对称轴为x=2，则a=______。

答 案：4  

解 析：本题主要考查的知识点为二次函数的性质。 由题意，该函数图像的对称轴为得a=4。

2、过点（2，0）作圆x2+y2=1的切线，切点的横坐标为（）。

答 案：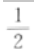

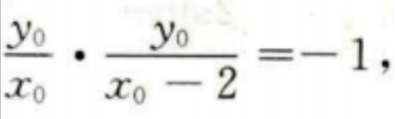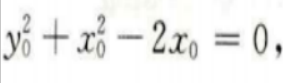
解 析：本题主要考查的知识点为圆的切线. 设切点(x0,y0)则有 即所以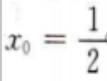故切点横坐标为