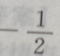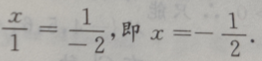单选题
1、设α是第三象限角,若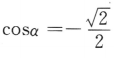 ,则sinα=()
,则sinα=()
- A:
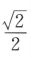
- B:

- C:
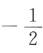
- D:
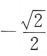
答 案:D
解 析:由于 ,而α为第三象限角,故
,而α为第三象限角,故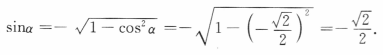
2、已知偶函数y=f(x),在区间[a,b](0 答 案:B 解 析:由偶函数的性质:偶函数在[a,b]和[-b,-a]上有相反的单调性,可知,y=f(x)在区间[a,b](0 3、已知空间向量i,j,k为两两垂直的单位向量,向量a=2i+3j+mk,若 答 案:C 解 析:由题可知向量a=(2,3,m),故 4、袋中有6个球,其中4个红球,2个白球,从中随机取出2个球,则其中恰有1个红球的概率为() 答 案:A 解 析: 主观题 1、在正四棱柱ABCD-A'B'C'D'中, 答 案:(Ⅰ)由题意知(如图所示) 2、已知等差数列{an}中,a1+a2+a3=6,a2+a4+a5= 12求{an}的首项与公差。
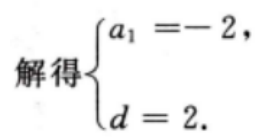
答 案:因为{an}为等差数列, 3、已知直线l的斜率为1,l过抛物线C: 答 案:(I)C的焦点为 4、已知数列 答 案: 填空题 1、九个学生期末考试的成绩分别为79 63 88 94 99 77 89 81 85这九个学生成绩的中位数为______。
答 案:85
解 析:本题主要考查的知识点为中位数. 将成绩按由小到大排列:63,77,79,81,85,88,89,94,99.因此中位数为85。 2、若平面向量a=(x,1),b=(1,-2),且a//b,则x=()
答 案: 解 析:由于a//b,故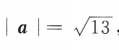 ,则m=()
,则m=()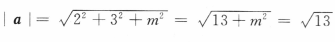 ,解得m=0.
,解得m=0.
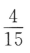

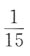
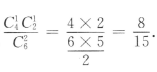
 (Ⅰ)写出向量
(Ⅰ)写出向量 关于基底{a,b,c}的分解式
(Ⅱ)求证:
关于基底{a,b,c}的分解式
(Ⅱ)求证: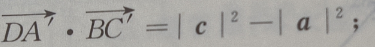 (Ⅲ)求证:
(Ⅲ)求证: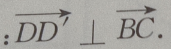
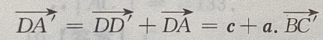
 (Ⅱ)
(Ⅱ)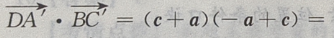
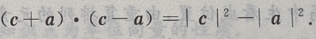 (Ⅲ)
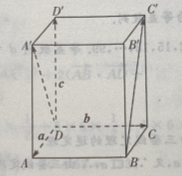
(Ⅲ)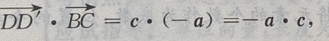 由已知,a,c是正四棱柱的棱,a,b,c两两垂直
由已知,a,c是正四棱柱的棱,a,b,c两两垂直

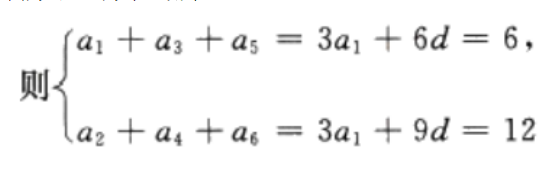
 的焦点,且与C交于A,B两点.(I)求l与C的准线的交点坐标;
的焦点,且与C交于A,B两点.(I)求l与C的准线的交点坐标;
(II)求|AB|. ,准线为
,准线为 由题意得l的方程为
由题意得l的方程为 因此l与C的准线的交点坐标为
因此l与C的准线的交点坐标为 (II)由
(II)由 ,得
,得 设A(x1,y1),B(x2,y2),则
设A(x1,y1),B(x2,y2),则 因此
因此
 的前n项和
的前n项和 求证:
求证: 是等差数列,并求公差和首项。
是等差数列,并求公差和首项。