单选题
1、要求设计实验证明某种盐的水解是吸热的,有四位同学分别做出如下回答,其中正确的是( )。
答 案:D
解 析:因硝酸铵晶体溶于水吸收热量,则水温下降,不能说明盐水解为吸热反应;中和反应为放热反应,且一水合氨的电离过程为吸热反应,不能说明盐类水解是吸热的;醋酸钠溶液中加入醋酸钠晶体,醋酸根离子浓度增大,促进水解,溶解过程伴随热效应,则不能说明盐类水解是吸热的;醋酸钠溶液中滴入酚酞溶液,加热后若红色加深,则说明升高温度可以促进盐类水解,因此可以证明盐类水解为吸热反应。"
2、微分方程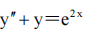 的一个特解是()。
的一个特解是()。
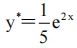
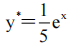
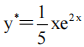
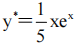
答 案:A
解 析:可验证,四个选项中只有A项满足微分方程,故其特解为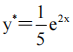 .
.
3、设z=x3y,则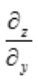 =().
=().

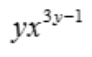
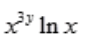
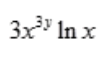
答 案:D
解 析:将x看为常数,因此z为y的指数函数,可知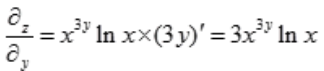 。
。
主观题
1、设函数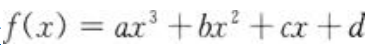 ,问常数a,b,c满足什么关系时,f(x)分别没有极值、可能有一个极值、可能有两个极值?
,问常数a,b,c满足什么关系时,f(x)分别没有极值、可能有一个极值、可能有两个极值?
答 案:解:此函数在定义域(-∞,+∞)处处可导,因此,它的极值点必是驻点即导数等于零的点,求导得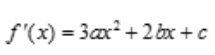 令
令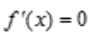 即
即 由一元二次方程根的判别式知:当
由一元二次方程根的判别式知:当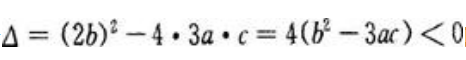 时,
时,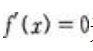 无实根。
无实根。
由此可知,当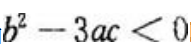 时,f(x)无极值。
时,f(x)无极值。
当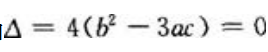 时,
时,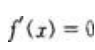 有一个实根。
有一个实根。
由此可知,当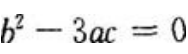 时,f(x)可能有一个极值。
时,f(x)可能有一个极值。
当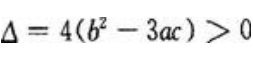 时,f(x)可能有两个极值。
时,f(x)可能有两个极值。
2、设函数f(x)=x-lnx,求f(x)的单调增区间.
答 案:解:函数f(x)的定义域为(0,+∞)。令y=f(x),则 令y'=0,解得x=1。当0<x<1时,y'<0;当x>1时,y'>0。
令y'=0,解得x=1。当0<x<1时,y'<0;当x>1时,y'>0。
因此函数f(x)的单调增区间为(1,+∞)。
3、设 求C的值。
求C的值。
答 案:解: 则
则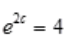 ,有
,有 ,
, 。
。
填空题
1、设区域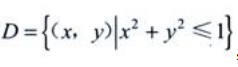 ,则
,则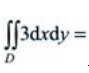 ()。
()。
答 案:3π
解 析:积分区域D为半径为1的圆域,其面积为π,因此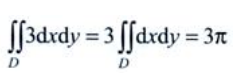 。
。
2、设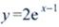 ,则y'=()。
,则y'=()。
答 案: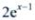
解 析: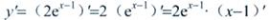

3、幂级数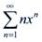 的收敛半径R=()。
的收敛半径R=()。
答 案:1
解 析:对于级数 ,
,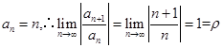 ,
,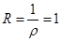 。
。
简答题
1、设f(x)=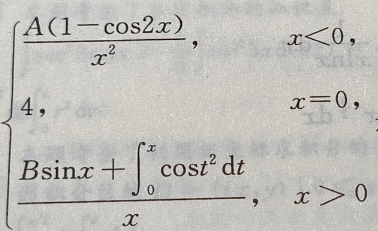 在x=0连续,试确定A,B.
在x=0连续,试确定A,B.
答 案: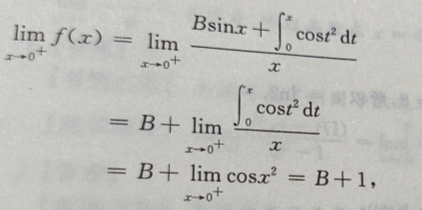
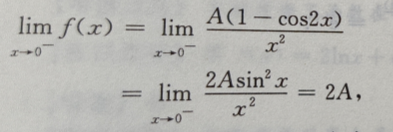 欲使f(x)在x=0处连续,应有2A=4=B+1,所以A=2,B=3.
欲使f(x)在x=0处连续,应有2A=4=B+1,所以A=2,B=3.