判断题
1、若
，则
。（）
答 案：错
解 析：
所以
单选题
1、设离散型随机变量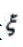
的分布列为
，则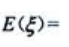
（）.
答 案：A
解 析：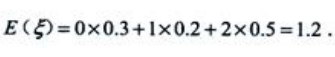
2、函数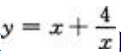
的单调减少区间为（）.
答 案：D
解 析：由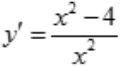
，令y'=0得驻点为（2，±2），而不可导点为x＝0.列表讨论如下：
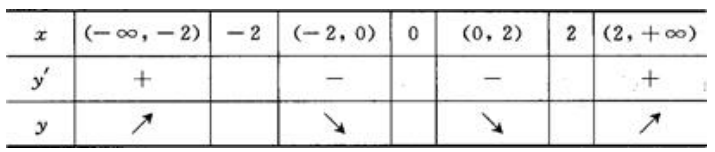所以单调减少区间为（-2，0）和（0，2）.
主观题
1、设函数y＝sinx2＋2x，求dy．
答 案：解：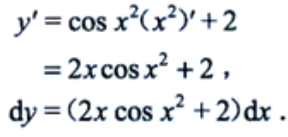
2、设曲线y＝cosx（0≤x≤π/2）与x轴、y轴所围成的图形面积被曲线y＝asinx，y＝bsinx（a＞b＞0）三等分，试确定a、b的值．
答 案：解：由y＝cosx，y＝asinx，得tanx＝1/a，故有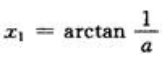
；同理可求得
.因为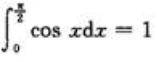
，令这三部分的面积分别为D1，D2，D3，有D1＝D2＝D3＝1/3．
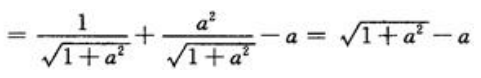，故a＝4/3．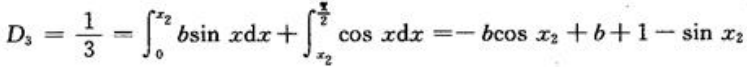
故b＝5/12．
填空题
1、设
，则
（）
答 案：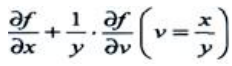
解 析：设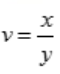
，则z＝f（x，v），则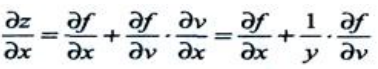
2、若
则
=（）
答 案：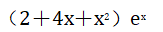
解 析：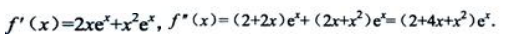
简答题
1、盒中有5个球，其中3个白球，2个黑球，从中随机一次抽取3个球，用X表示抽取到的白球的个数。 （1）求随机变量X的概率分布；
（2）求X的数学期望E（X）.
答 案：
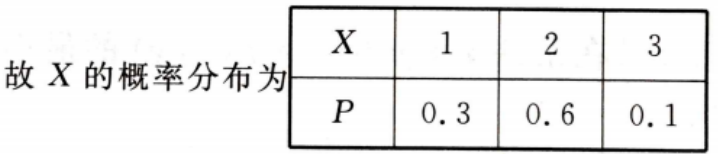(2)E(X)=1x0.3+2x0.6+3x0.1=1.8.
2、证明：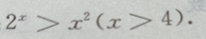
答 案：令
则
由于此式不便判定符号，故再求出
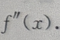又因
所以f'(x)单调增加，故f'(x)>f'(4)=
-8=8(2ln2-1)=8(ln4-1)>0, 得到f(x)单调增加，故f(x)>f(4),即
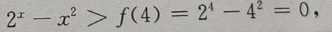因此
