单选题

1、设集合 （）。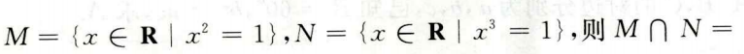

• A：{1}
• B：{-1}
• C：{—1，1）
• D：

答 案：A

解 析：本题主要考查的知识点为集合的运算。 由题意M={-1，1}，N={1}，所以M∩N=（1}。  

2、（）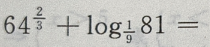  

• A：8
• B：14
• C：12
• D：10

答 案：B

解 析：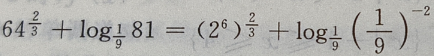

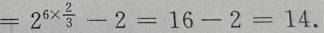
3、直线2x-y+7=0,与圆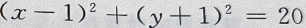的位置关系是（）  

• A：相离
• B：相交但不过圆心
• C：相切
• D：相交且过圆心

答 案：C

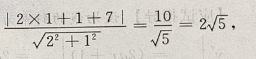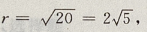解 析：易知圆心坐标（1，-1），圆心到直线2x-y+7=0的距离d ∵圆的半径 ∴d=r，∴直线与圆相切  

4、已知点M（1，2），N（2，3），则直线MN的斜率为（）。

• A：
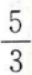
• B：1
• C：-1
• D：

答 案：B

解 析：本题主要考查的知识点为直线的斜率。 直线MN的斜率为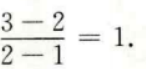

主观题

1、如图：已知在△ADC中，∠C=90°，∠D=30°，∠ABC=45°，BD=20，求AC(用小数表示，保留一位小数)  

答 案：如图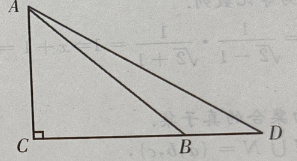  

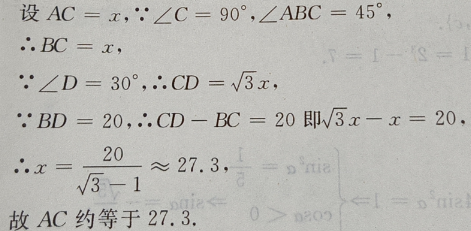
2、设椭圆的中心是坐标原点,长轴在x轴上,离心率已知点P到圆上的点的最远距离是求椭圆的方程  

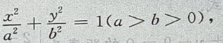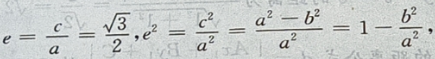
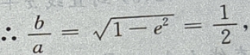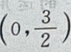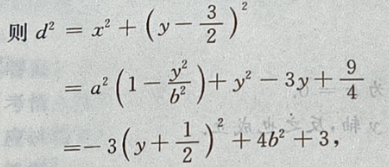
答 案：由题意，设椭圆方程为 由 设P点到椭圆上任一点的距离为 d, 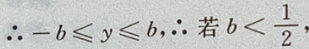则在y=-b时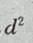，最大，即d也最大。  

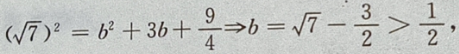
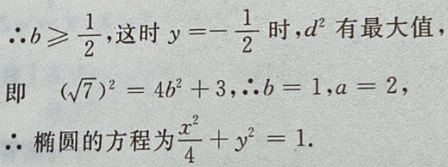
3、已知三角形的一个内角是，面积是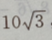周长是20,求各边的长.  

答 案：设三角形三边分别为a,b,c,∠A=60°，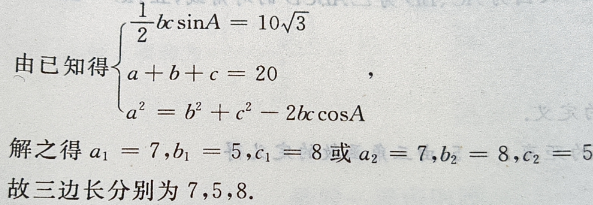  

4、已知函数f（x）=（x-4）（x2-a）。（I）求f’（x）；
（Ⅱ）若f’（-1）=8，求f（x）在区间[0，4]的最大值与最小值。

答 案：(I)f'(x) =(x-4)'(x²-a)+(x-4)(x²-a)’ =x²-a+2x(x-4) =3x²-8x-a. (Ⅱ)由于f’(-1)=3+8-a=8,得a=3. 令f'(x)=3x²-8x-3=0,解得x1=3，（舍去）又f（0）=12，f（3）=-6，f（4）=0所以在区间[0，4]上函数最大值为12，最小值为-6

填空题

1、不等式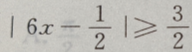的解集是（）  

答 案：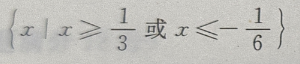

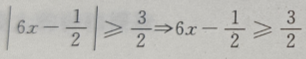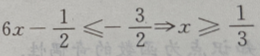解 析：或或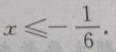

2、（）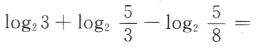

答 案：3

解 析：