单选题
1、设y＝f（x）为分段函数，x0为其分段点，且函数在x0处连续，则下列命题（）正确。
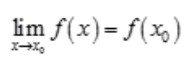
答 案：C
解 析：函数在x0处连续，即在x0处f(x)的左右极限存在且相等，所以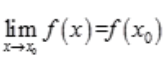
。
2、微分方程y'＋y＝0的通解为y＝（）。
答 案：C
解 析：所给方程为可分离变量方程，分离变量得
。两端分别积分
。
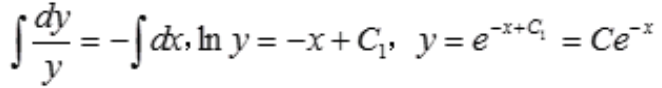3、下列四个点钟，在平面x+y-z+2=0上的是（）
答 案：A
解 析：把选项中的几个点带入平面方程,只有选项 A 满足方程,故选项 A是平面上的点.
主观题
1、计算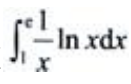
．
答 案：解：
2、求函数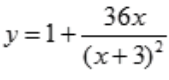
的凹凸性区间及拐点．
答 案：解：函数的定义域为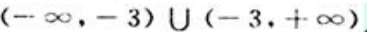
。
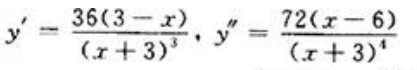．令y″＝0，得x＝6；不可导点为x＝－3。故拐点为（6，
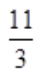），（－∞，－3）和（－3,6）为凸区间，（6，＋∞）为凹区间。
3、求过点M0（0，2，4），且与两个平面π1，π2都平行的直线方程，其中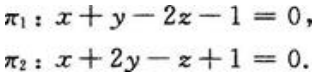
答 案：解：如果直线l平行于π1，则平面π1的法线向量n1必定垂直于直线l的方向向量s．同理，直线l平行于π2，则平面π2的法线向量n2必定满足n2⊥s．由向量积的定义可知，取
由于直线l过点M0（0，2，4），由直线的标准方程可知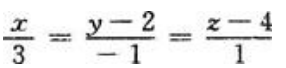
为所求直线方程。
填空题
1、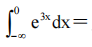
（）
答 案：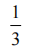
解 析：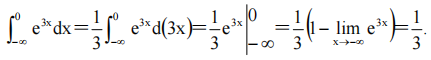
2、幂级数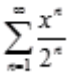
的收敛区间（不考虑端点）是（）。
答 案：（－2，2）
解 析：
，因此R＝
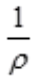＝2，所以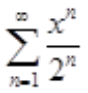
的收敛区间为（－2，2）。
3、交换二次积分的积分次序，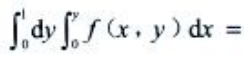
（）。
答 案：
解 析：由题设有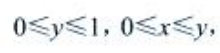
从而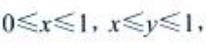
故交换次序后二次积分为
。
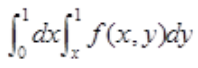简答题
1、求函数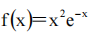
的单调区间和极值.
答 案：
由表可知，函数的单调曾区间为（0，2）；单调减区间为（-∞，0），（2，+∞）
极大值为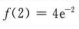
，极小值为f（0）=0.
