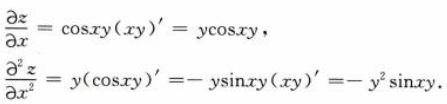单选题
1、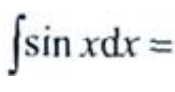 ()。
()。
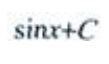
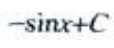
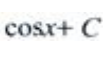

答 案:D
解 析:由不定积分的基本积分公式可得,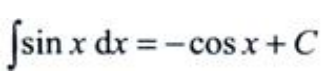 。
。
2、设函数,f(x)在[a,b]上连续,且F/(x)=f(x),有一点x0∈(a,b)使,f(x0)=0,且当a≤x≤x0时,f(x)>0;当x0<x≤b时,f(x)<0,则f(x)与x=a,x=b,x轴围成的平面图形的面积为()。
答 案:A
解 析:由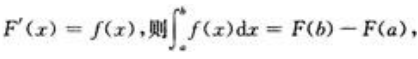 而f(x)与x=a,x=b,X轴围成的平面图形的面积为
而f(x)与x=a,x=b,X轴围成的平面图形的面积为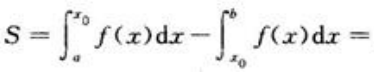

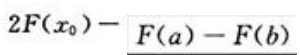 。
。
3、设函数 ,则f(x)的导数f'(x)=()。
,则f(x)的导数f'(x)=()。



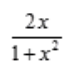
答 案:C
解 析:由可变限积分求导公式 可知
可知
主观题
1、设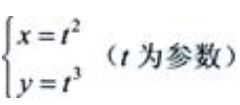 ,求
,求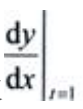
答 案:解:由题意得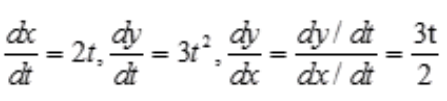 故
故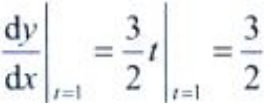 。
。
2、已知f(π)=1,且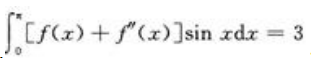 ,求f(0)。
,求f(0)。
答 案:解:
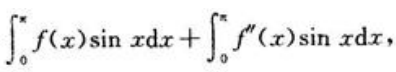 对
对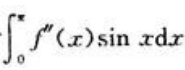 采用凑微分和分部积分后与
采用凑微分和分部积分后与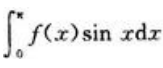 相加,代入条件即可求出f(0)。因为
相加,代入条件即可求出f(0)。因为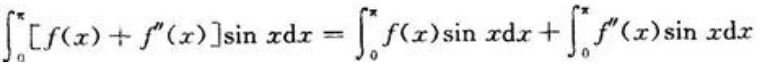
而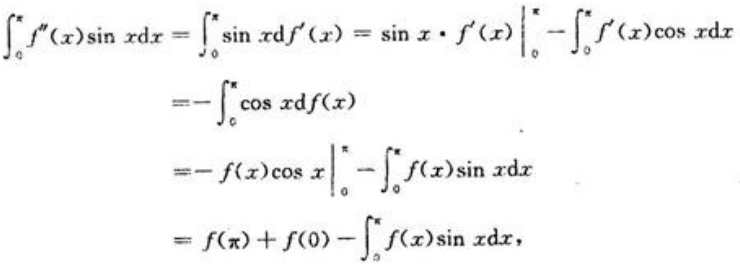
所以
又f(π)=1,所以f(0)=2。
3、计算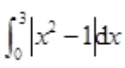 。
。
答 案:解:
填空题
1、二阶常系数齐次线性方程y''=0的通解为()。
答 案: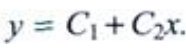
解 析:y''=0特征方程为r2=0特征根为r=0(二重根),于是二阶常系数齐次线性方程的通解为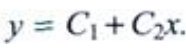
2、过点M0(1,-2,0)且与直线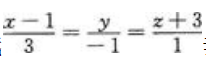 垂直的平面方程为()。
垂直的平面方程为()。
答 案:3(x-1)-(y+2)+x=0(或3x-y+z=5)
解 析:因为直线的方向向量s=(3,-1,1),且平面与直线垂直,所以平面的法向量 ,由点法式方程有平面方程为:3(x-1)-(y+2)+(z-0)=0,即3(x-1)-(y+2)+z=0。
,由点法式方程有平面方程为:3(x-1)-(y+2)+(z-0)=0,即3(x-1)-(y+2)+z=0。
3、已知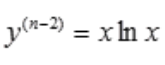 ,则
,则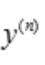 =()。
=()。
答 案: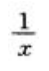
解 析:因为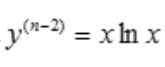 ,故
,故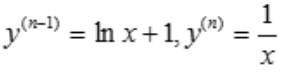 。
。
简答题
1、设z=sinxy,求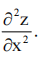
答 案: