2024年成考专升本《高等数学二》每日一练试题05月18日
考试问答
2024-05-18
11:23:17
收藏
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
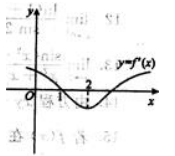
1、根据f(x)的导函数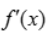 的图像(如图所示),判断下列结论正确的是( ).
的图像(如图所示),判断下列结论正确的是( ).
- A:在(∞,1)上f(x)是单调递减的
- B:在(∞,2)上f(x)是单调递减的
- C:f(1)为极大值
- D:f(1)为极小值
答 案:C
解 析:在x轴上方的曲线是表示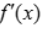 >0,而x轴下方的曲线则表示
>0,而x轴下方的曲线则表示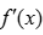 <0,注在x=1处的左边即x<1时
<0,注在x=1处的左边即x<1时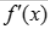 >0,而2>x>1时
>0,而2>x>1时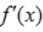 <0,根据极值的第一充分条件可知f(1)为极大值.
<0,根据极值的第一充分条件可知f(1)为极大值.
2、设f(x)在点x0处连续,则().
- A:f'(x)一定存在
- B:f'(x)一定不存在
- C:
 一定存在
一定存在 - D:
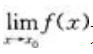 不一定存在
不一定存在
答 案:C
解 析:A项, 在x=0处连续,但在x=0处导数不存在;B项,
在x=0处连续,但在x=0处导数不存在;B项,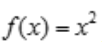 在x=0处连续,导数也存在;CD两项,在x0处连续即左极限=右极限=f(x0),所以极限一定存在.
在x=0处连续,导数也存在;CD两项,在x0处连续即左极限=右极限=f(x0),所以极限一定存在.
主观题
1、设函数y=ln(x2+1),求dy.
答 案:解: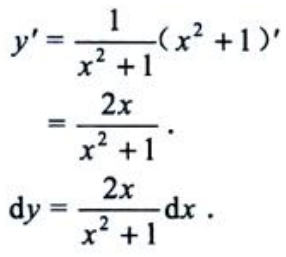
2、某射手击中10环的概率为0.26,击中9环的概率为0.32,击中8环的概率为0.36,求在一次射击中不低于8环的概率.
答 案:解:设A={击中10环),B={击中9环),C={击中8环),D={击中不低于8环),则D=A+B+C,由于A,B,C相互独立,所以P(D)=P(A+B+C)=P(A)+P(B)+P(C)=0.26+0.32+0.36=0.94
填空题
1、曲线y=2x2在点(1,2)处的切线方程为y=().
答 案:4x-2
解 析: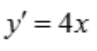 ,
,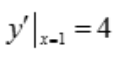 ,故切线方程为
,故切线方程为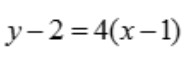 ,即
,即 .
.
2、 ().
().
答 案:
解 析:因为积分区间关于原点对称,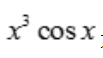 是奇函数,故
是奇函数,故 ,则
,则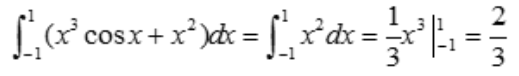
简答题
1、设函数y=sin2x,求
答 案: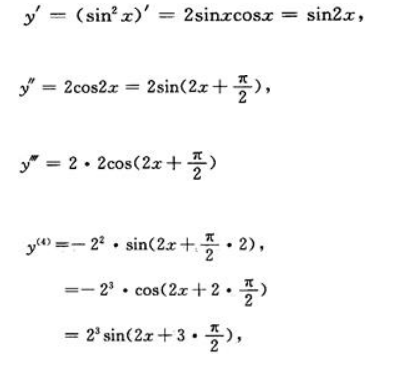 所以
所以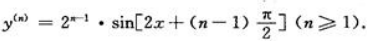
2、计算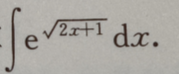
答 案:
更多推荐

