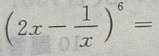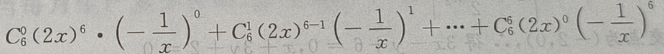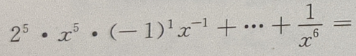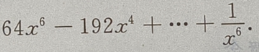单选题
1、下列函数中,为奇函数的是()
- A:
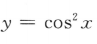
- B:
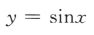
- C:
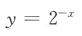
- D:
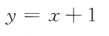
答 案:B
解 析:当f(-x)=-f(x),函数f(x)是奇函数,只有选项B符合.
2、已知向量a=(3,4),向量 b=(0,-2),则cos的值为()
- A:
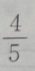
- B:
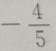
- C:

- D:
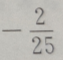
答 案:B
解 析:求cos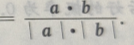 a·b=(3,4)·(0,-2)=3×0+4×(-2)=8,
a·b=(3,4)·(0,-2)=3×0+4×(-2)=8,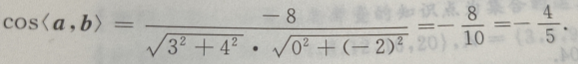
3、在△ABC中,若b=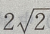 ,c=
,c=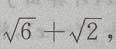
 则a等于()
则a等于()
- A:2
- B:
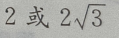
- C:
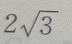
- D:无解
答 案:B
解 析:此题是已知两边和其中一边的对角,解三角形时,会出现一解、两解、无解的情况,要注意这一点.用余弦定理 可得
可得

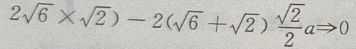
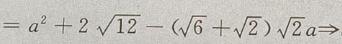
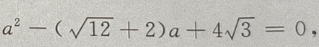 解出
解出


4、设f(x)=x3+ax2+x为奇函数,则a=()。
- A:1
- B:0
- C:
- D:-2 D.C.-1
答 案:B
解 析:本题主要考查的知识点为函数的奇偶性. 因为f(x)为奇函数,故f(-x)=-f(x)。即-x3+ax2-x=-x3-ax2-x,a=0。
主观题
1、记△ABC的内角A,B,C的对边分别为a,b,c,已知B=60°,b2=ac,求A。
答 案:由余弦定理b2=a2+c2-2accosB,可得ac=a2+c2-ac,即a2+c2-2ac=(a-c)2=0,解得a=c。 又因为B=60°,故△ABC为等边三角形,所以A=60°
2、已知抛物线C:y2=2px(p>0)的焦点到准线的距离为1。 (I)求C的方程; (Ⅱ)若A(1,m)(m>0)为C上一点,O为坐标原点,求C上另一点B的坐标,使得OA⊥OB
答 案:(I)由题意,该抛物线的焦点到准线的距离为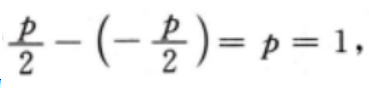 所以抛物线C的方程为
所以抛物线C的方程为 (Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得
(Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得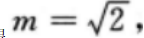 因此A点坐标为
因此A点坐标为 设B点坐标为
设B点坐标为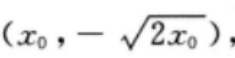 则
则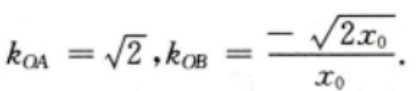 因为
因为 则有
则有 即
即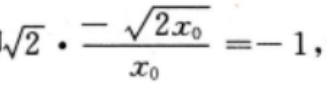 解得x0=4
所以B点的坐标为
解得x0=4
所以B点的坐标为
3、在正四棱柱ABCD-A'B'C'D'中, (Ⅰ)写出向量
(Ⅰ)写出向量 关于基底{a,b,c}的分解式
(Ⅱ)求证:
关于基底{a,b,c}的分解式
(Ⅱ)求证: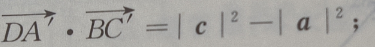 (Ⅲ)求证:
(Ⅲ)求证: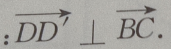
答 案:(Ⅰ)由题意知(如图所示) 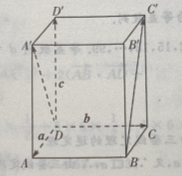
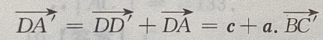
 (Ⅱ)
(Ⅱ)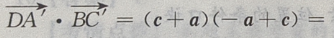
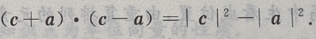 (Ⅲ)
(Ⅲ)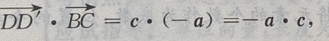 由已知,a,c是正四棱柱的棱,a,b,c两两垂直
由已知,a,c是正四棱柱的棱,a,b,c两两垂直

4、设函数f(x)=xlnx+x.(I)求曲线y=f(x)在点((1,f(1))处的切线方程;
(II)求f(x)的极值.
答 案:(I)f(1)=1,f'(x)=2+lnx,故f'(1)=2.所以曲线y=f(x)在点(1,f(1))处的切线方程为y=2x-1.(II)令f'(x)=0,解得 当
当 时,f'(x)
时,f'(x) 单调递减,在区间
单调递减,在区间 单调递增.因此f(x)在
单调递增.因此f(x)在 时取得极小值
时取得极小值
填空题
1、若平面向量a=(x,1),b=(1,-2),且a//b,则x=()
答 案: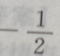
解 析:由于a//b,故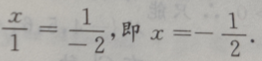
2、 的展开式是()
的展开式是()
答 案: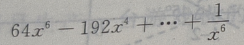
解 析: