判断题

1、若，则。（）  

答 案：错

解 析：所以  

单选题

1、已知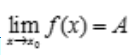，则点x₀是函数f（x）的（）.

• A：间断点
• B：连续点
• C：可导点
• D：连续性不确定的点

答 案：D

解 析：因为中的A不一定等于函数值f（x₀），所以在x₀处的连续性是不确定的.

2、（）.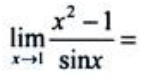

• A：0
• B：1
• C：
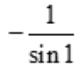
• D：2

答 案：A

解 析：.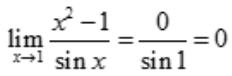

主观题

1、证明：当x＞1时，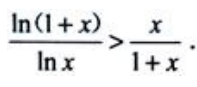

答 案：证：设F(x)＝(1＋x)ln(1＋ｘ)－xlnx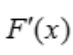．＝ln(1＋x)＋1－lnx－１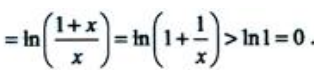所以，当ｘ＞1时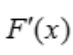，＞0，即F(ｘ)单调增加．
当x＞1时，F(x)＞F(1)＝2ln2＞0，即(1＋x)ln(1＋ｘ)－ｘlnｘ＞0．所以.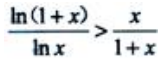

2、证明：当x＞0时，

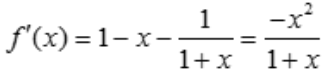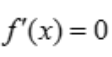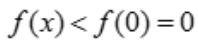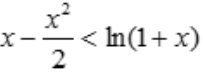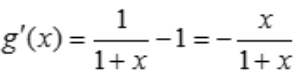答 案：证：令，，令，得x＝0，f(0)=0，当x＞0时，f'(x)＜0，故函数单调递减，，则．令，，令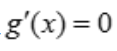，得x＝0，g(0)=0，当x＞0时，f'(x)＜0，故函数单调递减，f(x)＜f(0)=0，则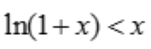．综上得，当x＞0时，．

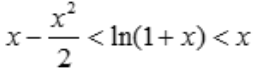填空题

1、（）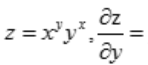

答 案：

解 析：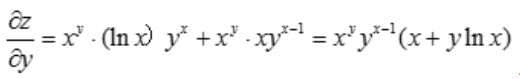

2、（）．

答 案：x＋arctanx

解 析：．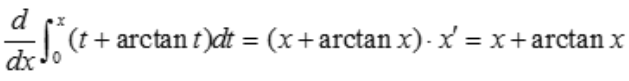

简答题

1、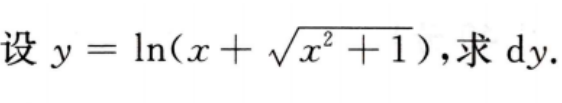

答 案：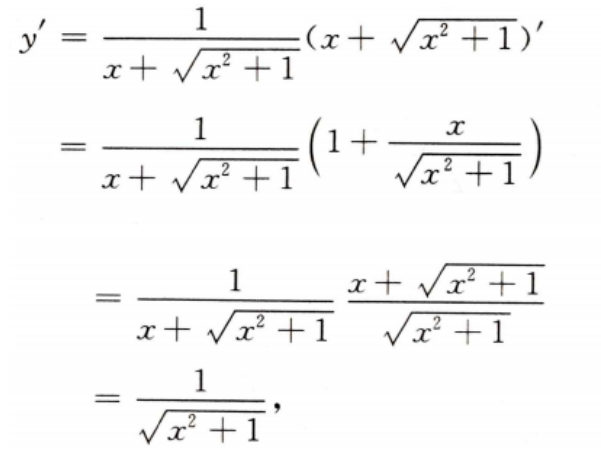

2、设离散型随机变量X的概率分布为 （1）求X的分布函数F（x）；（2）求E（X）.  

答 案：（1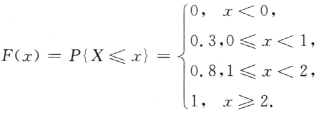）（2）E(X)=0×0.3＋1×0.5＋2×0.2=0.9.