判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
1、设f'(x)在-闭区间[0,1]上连续,则曲线y=f(x)与直线x=0,x=1和y=0所围成的平面图形的面积等于()
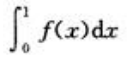
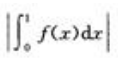
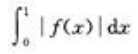
答 案:C
解 析:由定积分的几何意义可知,当在区间[a,b]上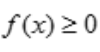 时,
时,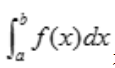 表示曲线y=f(x)与两条直线x=a,x=b以及x轴所围成的曲边梯形的面积;当在区间[a,b]上
表示曲线y=f(x)与两条直线x=a,x=b以及x轴所围成的曲边梯形的面积;当在区间[a,b]上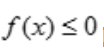 时,
时,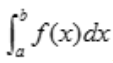 表示曲线y=f(x)与两条直线x=a,x=b以及x轴所围成的曲边梯形面积的负值
表示曲线y=f(x)与两条直线x=a,x=b以及x轴所围成的曲边梯形面积的负值
2、设 ,则
,则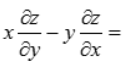 ()
()
答 案:C
解 析:
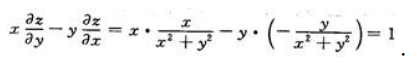
主观题
1、已知函数f(x)=-x2+2x.(1)求曲线y=f(x)与x轴所围成的平面图形的面积S;
(2)求(1)中的平面图形绕x轴旋转一周所得旋转体的体积V.
答 案:解:(1)由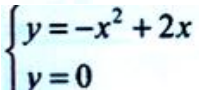 得曲线与x轴交点坐标为(0,0),(2,0).
得曲线与x轴交点坐标为(0,0),(2,0). (2)
(2)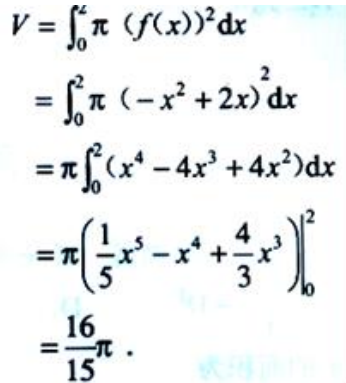
2、设函数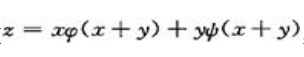 ,其中
,其中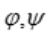 有二阶偏导数.
有二阶偏导数.
答 案:证明: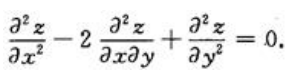 证:对x求导,
证:对x求导, 再对x求导,得
再对x求导,得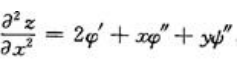 ;
; 对y求导,得
对y求导,得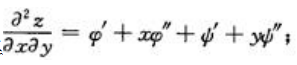 类似可得,
类似可得,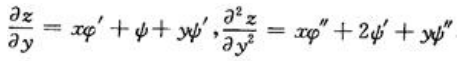 ;所以
;所以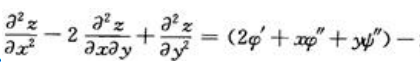
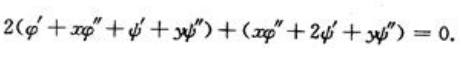
填空题
1、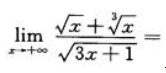 ()
()
答 案: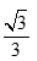
解 析: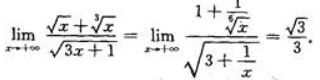
2、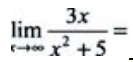 ().
().
答 案:
解 析:由洛必达法则有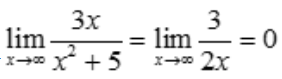 .
.
简答题
1、证明:当x≥0时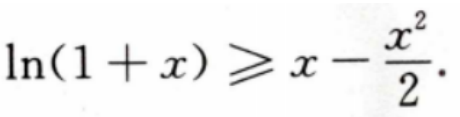
答 案:令f(x)=ln(1+x)-x+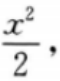 则f’(x)=
则f’(x)=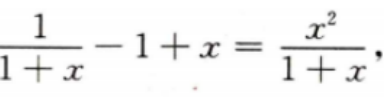 当x≥0时,f’(x)≥0,因此,当x≥0时,f(x)为单调增函数,故有f(x)≥f(0)=0,故当x≥0时,
当x≥0时,f’(x)≥0,因此,当x≥0时,f(x)为单调增函数,故有f(x)≥f(0)=0,故当x≥0时,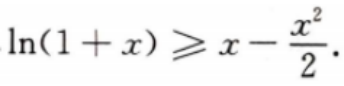
2、求曲线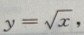 直线x=1和x轴所围成的有界平面图形的面积S,及该平面图形绕x轴旋转一周所得旋转体的体积V。
直线x=1和x轴所围成的有界平面图形的面积S,及该平面图形绕x轴旋转一周所得旋转体的体积V。
答 案: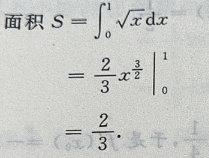
解 析: