单选题
1、若级数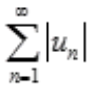 收敛,则
收敛,则 ()。
()。
答 案:C
解 析:级数绝对收敛的性质可知, 收敛,则
收敛,则 收敛,且为绝对收敛。
收敛,且为绝对收敛。
2、当n→∞时,下列变量为无穷小量的是()。
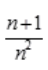
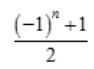
答 案:A
解 析:A项,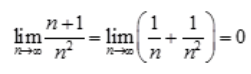 ;B项,
;B项,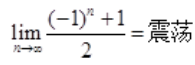 ;C项,
;C项, ;D项,
;D项,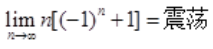 。
。
3、下列等式成立的是()
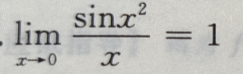
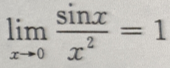
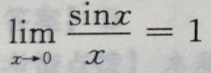
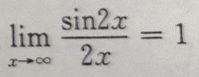
答 案:C
解 析:由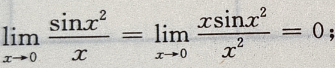
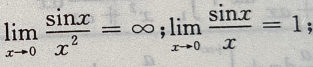
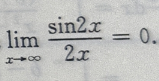
主观题
1、设z=f(x,y)是由方程 所确定,求
所确定,求 。
。
答 案:解:由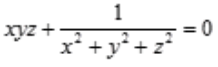 得全微分方程:
得全微分方程: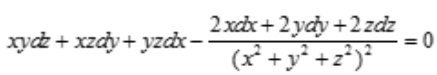 化简得
化简得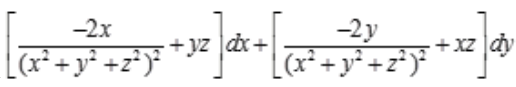
 所以
所以
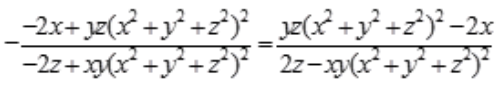 。
。
2、设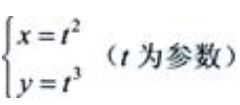 ,求
,求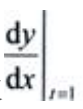
答 案:解:由题意得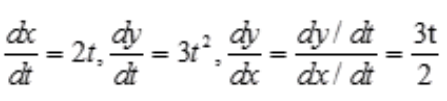 故
故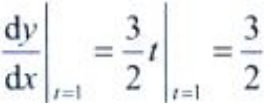 。
。
3、求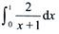 .
.
答 案:解: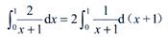
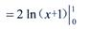 =2ln2
=2ln2
填空题
1、设函数z=f(x,y)可微,(x0,y0)为其极值点,则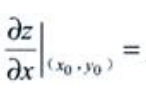 ()。
()。
答 案:
解 析:由于z=f(x,y)可微,则偏导数必定存在,再由二元函数极值的必要条件可知,若点(x0,y0)为z=f(x,y)的极值点,且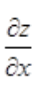 ,
, 在点(x0,y0)处存在,则必有
在点(x0,y0)处存在,则必有
2、定积分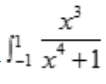 dx=()。
dx=()。
答 案:
解 析:因为 是奇函数,所以定积分
是奇函数,所以定积分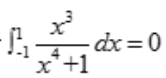 。
。
3、过点M(1,2,-1)且与平面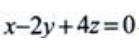 垂直的直线方程为()。
垂直的直线方程为()。
答 案: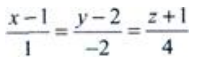
解 析:由于直线与平面x-2y+4z=0垂直,可取直线方向向量为(1,-2,4),因此所求直线方程为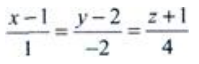
简答题
1、若函数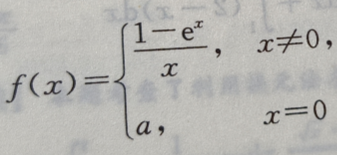 在x=0处连续。求a。
在x=0处连续。求a。
答 案:由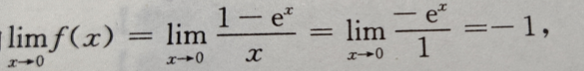 又因f(0)=a,所以当a=-1时,f(x)在x=0连续。
又因f(0)=a,所以当a=-1时,f(x)在x=0连续。