2024年成考专升本《高等数学二》每日一练试题05月05日
考试问答
2024-05-05
11:23:47
收藏
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
1、设函数z=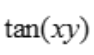 ,则
,则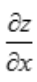 ().
().
- A:
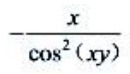
- B:
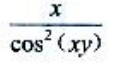
- C:
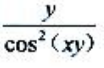
- D:
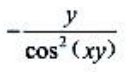
答 案:C
解 析: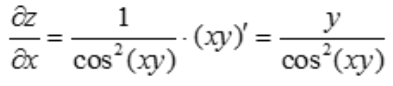 .
.
2、箱子中有2个红球,3个白球,从中任取2球,则取到的球是一红一白的概率是().
- A:0.3
- B:0.4
- C:0.6
- D:1/3
答 案:C
解 析:根据排列组合的知识可知,取到的球是一红一白的概率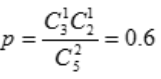 .
.
主观题
1、求 .
.
答 案:解:
2、某班有党员10人,其中女党员有6人,现选3人组成党支部.设事件A={党支部中至少有1名男党员},求P(A).
答 案:解: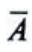 ={党支部中没有男党员},则
={党支部中没有男党员},则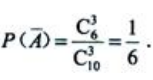 因为
因为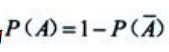 ,所以
,所以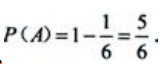
填空题
1、函数f(x)= 的连续区间为().
的连续区间为().
答 案: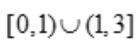
解 析: 所以在x=1处f(x)不连续.在x=2处
所以在x=1处f(x)不连续.在x=2处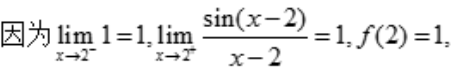 所以在x=2处f(x)连续,所以连续区间为
所以在x=2处f(x)连续,所以连续区间为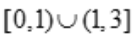 .
.
2、曲线y=2x2在点(1,2)处的切线方程为y=().
答 案:4x-2
解 析: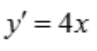 ,
,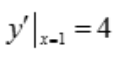 ,故切线方程为
,故切线方程为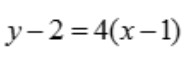 ,即
,即 .
.
简答题
1、某运动员投篮命中率为0.3,求一次投篮时投中次数的概率分布及分布函数
答 案:这次投篮的投中次数是随机变量,设其为X,他可能取得值为0,1,X=0表示投中0次,即投篮未中,P{X=0}=1-0.3=0.7,X=1表示投中一次,P{X=1}=0.3,故概率分布为: 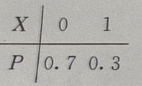 分布函数
分布函数
2、已知函数f(x)=ax3-bx2+cx在区间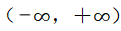 内是奇函数,且当x=1时,f(x)有极小值
内是奇函数,且当x=1时,f(x)有极小值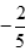 ,求另一个极值及此曲线的拐点.
,求另一个极值及此曲线的拐点.
答 案:f(x)=ax3-bx2+cx,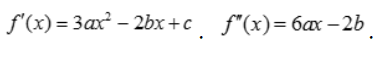 由于f(x)是奇函数,则必有x2的系数为0,即b=0.
由于f(x)是奇函数,则必有x2的系数为0,即b=0.
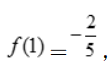 即a+c=
即a+c=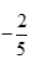 ,
,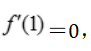 得3a+c=0.解得a=
得3a+c=0.解得a=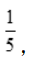 c=
c= 此时
此时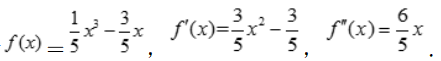 令
令 得
得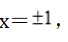
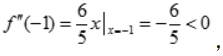 所以
所以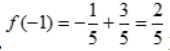 为极大值,
为极大值,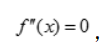 得x=0,x<0时,
得x=0,x<0时,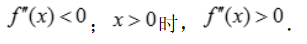 所以(0,0)为曲线的拐点.
所以(0,0)为曲线的拐点.
更多推荐

