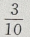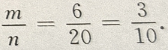单选题
1、设甲: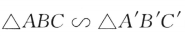 ;乙:
;乙: .则()
.则()
- A:甲是乙的必要条件但不是充分条件
- B:甲是乙的充分条件但不是必要条件
- C:甲是乙的充要条件
- D:甲既不是乙的充分条件也不是乙的必要条件
答 案:A
解 析:三角形相似不一定全等,但三角形全等一定相似,因此,甲是乙的必要条件但不是充分条件.
2、若x
答 案:D
解 析:本题主要考查的知识点为不等式的性质。 因为
3、在等比数列{an}中,a2=1,公比q=2,则a5=()。
- A:
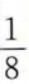
- B:
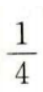
- C:4
- D:8
答 案:D
解 析:本题主要考查的知识点为等比数列。
4、函数 的图像与直线y=4的交点坐标为()
的图像与直线y=4的交点坐标为()
- A:(0,4)
- B:(4,64)
- C:(1,4)
- D:(4,16)
答 案:C
解 析:令y=4x=4,解得x=1,故所求交点为(1,4).
主观题
1、设函数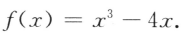
(I)求f'(2);
(II)求f(x)在区间[一1,2]的最大值与最小值.
答 案:(I)因为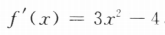 ,所以f'(2)=3×22-4=8.(II)因为x<-1,f(-1)=3.
,所以f'(2)=3×22-4=8.(II)因为x<-1,f(-1)=3.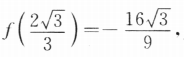 f(2)=0.
f(2)=0.
所以f(x)在区间[一1,2]的最大值为3,最小值为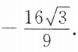
2、已知等差数列 前n项和
前n项和 (Ⅰ)求通项
(Ⅰ)求通项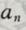 的表达式
(Ⅱ)求
的表达式
(Ⅱ)求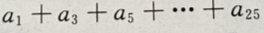 的值
的值
答 案:(Ⅰ)当n=1时,由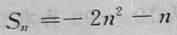 得
得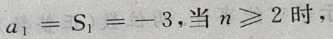
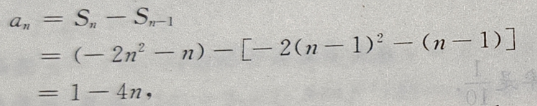
 也满足上式,故
也满足上式,故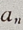 =1-4n(n≥1)
(Ⅱ)由于数列
=1-4n(n≥1)
(Ⅱ)由于数列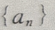 是首项为
是首项为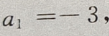 公差为d=-4的等差数列,所以
公差为d=-4的等差数列,所以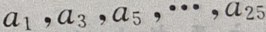 是首项为
是首项为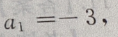 公差为d=-8,项数为13的等差数列,于是由等差数列前n项和公式得:
公差为d=-8,项数为13的等差数列,于是由等差数列前n项和公式得:

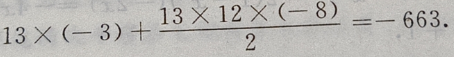
3、设函数f(x)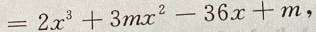 且f'(-1)=-36
(Ⅰ)求m
(Ⅱ)求f(x)的单调区间
且f'(-1)=-36
(Ⅰ)求m
(Ⅱ)求f(x)的单调区间
答 案:(Ⅰ)由已知得f'=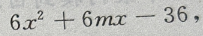 又由f'(-1)=-36得
6-6m-36=-36
故m=1.
(Ⅱ)由(Ⅰ)得f'(x)=
又由f'(-1)=-36得
6-6m-36=-36
故m=1.
(Ⅱ)由(Ⅰ)得f'(x)=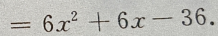 令f'(x)=0,解得
令f'(x)=0,解得 当x<-3时,f'(x)>0;
当-32时,f'(x)>0;
故f(x)的单调递减区间为(-3,2),f(x)的单调递增区间为(-∞,-3),(2,+∞)
当x<-3时,f'(x)>0;
当-32时,f'(x)>0;
故f(x)的单调递减区间为(-3,2),f(x)的单调递增区间为(-∞,-3),(2,+∞)
4、已知直线l的斜率为1,l过抛物线C: 的焦点,且与C交于A,B两点.
的焦点,且与C交于A,B两点.
(I)求l与C的准线的交点坐标;
(II)求|AB|.
答 案:(I)C的焦点为 ,准线为
,准线为 由题意得l的方程为
由题意得l的方程为 因此l与C的准线的交点坐标为
因此l与C的准线的交点坐标为 (II)由
(II)由 得
得 设A(x1,y1).B(x2,y2),则
设A(x1,y1).B(x2,y2),则 因此
因此
填空题
1、任选一个不大于20的正整数,它恰好是3的整数倍的概率是()
答 案: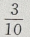
解 析:设n为不大于20的正整数的个数,则n=20,m为在这20个数中3的倍数:3,6、9、12、15、18的个数。 ∴m=6,∴所求概率=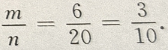
2、点(4,5)关于直线y=x的对称点的坐标为()
答 案:(5,4)
解 析:点(4,5)关于直线y=x的对称点为(5,4).
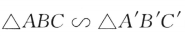 ;乙:
;乙: .则()
.则()
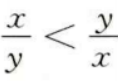



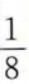
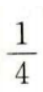

 的图像与直线y=4的交点坐标为()
的图像与直线y=4的交点坐标为()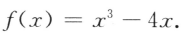
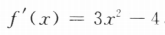 ,所以f'(2)=3×22-4=8.(II)因为x<-1,f(-1)=3.
,所以f'(2)=3×22-4=8.(II)因为x<-1,f(-1)=3.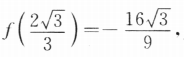 f(2)=0.
f(2)=0.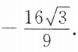
 前n项和
前n项和 (Ⅰ)求通项
(Ⅰ)求通项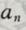 的表达式
(Ⅱ)求
的表达式
(Ⅱ)求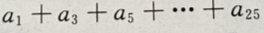 的值
的值
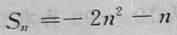 得
得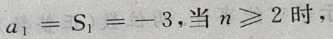
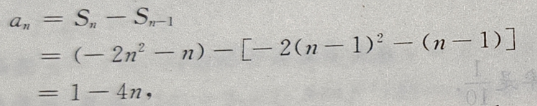
 也满足上式,故
也满足上式,故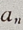 =1-4n(n≥1)
(Ⅱ)由于数列
=1-4n(n≥1)
(Ⅱ)由于数列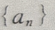 是首项为
是首项为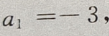 公差为d=-4的等差数列,所以
公差为d=-4的等差数列,所以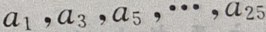 是首项为
是首项为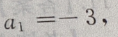 公差为d=-8,项数为13的等差数列,于是由等差数列前n项和公式得:
公差为d=-8,项数为13的等差数列,于是由等差数列前n项和公式得:

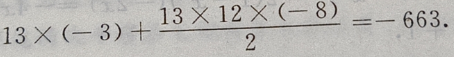
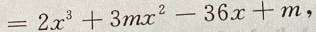 且f'(-1)=-36
(Ⅰ)求m
(Ⅱ)求f(x)的单调区间
且f'(-1)=-36
(Ⅰ)求m
(Ⅱ)求f(x)的单调区间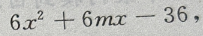 又由f'(-1)=-36得
6-6m-36=-36
故m=1.
(Ⅱ)由(Ⅰ)得f'(x)=
又由f'(-1)=-36得
6-6m-36=-36
故m=1.
(Ⅱ)由(Ⅰ)得f'(x)=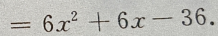 令f'(x)=0,解得
令f'(x)=0,解得 当x<-3时,f'(x)>0;
当-3
当x<-3时,f'(x)>0;
当-3 的焦点,且与C交于A,B两点.
的焦点,且与C交于A,B两点. ,准线为
,准线为 由题意得l的方程为
由题意得l的方程为 因此l与C的准线的交点坐标为
因此l与C的准线的交点坐标为 (II)由
(II)由 得
得 设A(x1,y1).B(x2,y2),则
设A(x1,y1).B(x2,y2),则 因此
因此