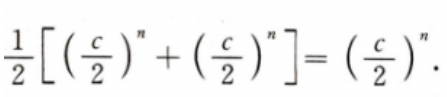判断题
1、若
，则
。（）
答 案：错
解 析：
所以
单选题
1、关于曲线
的铅垂渐近线，下面说法正确的是().
答 案：D
解 析：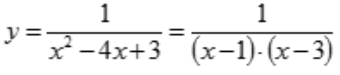
，可知x=1，x=3是曲线的间断点.
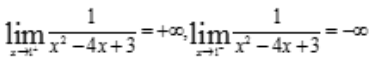，可知在x=1处是曲线的铅垂渐近线.
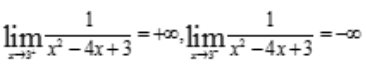，可知在x=3处是曲线的铅垂渐近线.
2、已知点A（5，2）为函数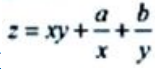
的极值点，则a，b分别为（）.
答 案：B
解 析：由极值存在的必要条件，应有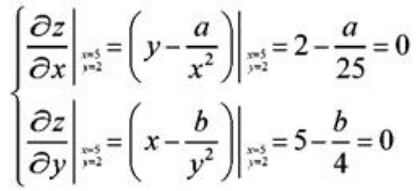
解得a＝50，b＝20.
主观题
1、求由曲线y＝ex，y＝e-x及x＝1所围成的平面图形的面积以及此平面图形绕x轴旋转一周所成的旋转体的体积Vx．
答 案：解：其平面图形如图所示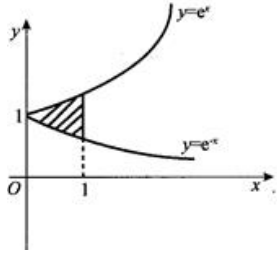
，则平面图形面积
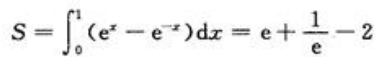旋转体的体积为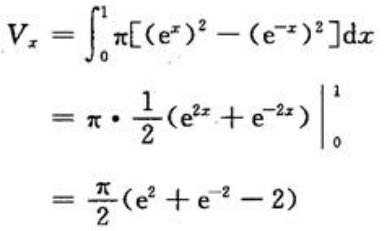
2、设z=f(x,y)是由方程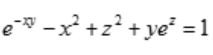
确定的函数，求
．
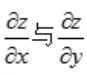答 案：解：x，y是自变量，而z＝z（x，y）．等式两边对x求导得
等式两边对y求导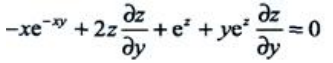得
解得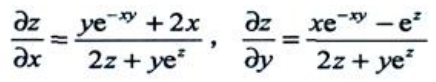
填空题
1、设函数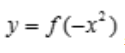
，且f(u)可导，则dy＝（）．
答 案：
解 析：因为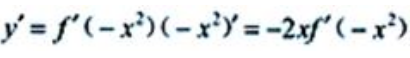
，所以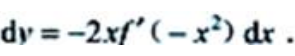
2、袋中有编号为1～5的5个小球，现从中任意取2个，则两个球的编号都不大于3的概率为（）．
答 案：0.3
解 析：两个球的编号都不大于3的有：1、2，1、3，2、3三种情况．从5个球中任取2个一共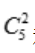
种情况．则两个球的编号都不大于3的概率为
．
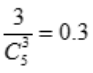简答题
1、证明：当x≥0时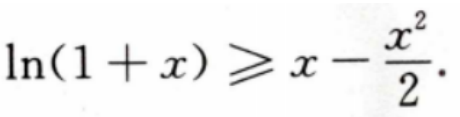
答 案：令f(x)=ln(1+x)-x+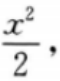
则f’(x)=
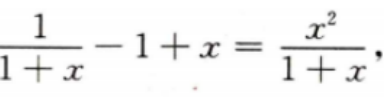当x≥0时，f’(x)≥0,因此，当x≥0时，f(x)为单调增函数，故有f(x)≥f(0)=0,故当x≥0时，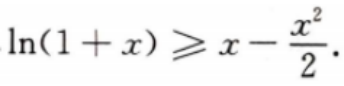
2、设函数f(x,y)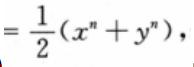
n为大于1的整数，求在条件x+y=c下f(x,y)得最小值，其中x＞0，y＞0，c为正常数。
答 案：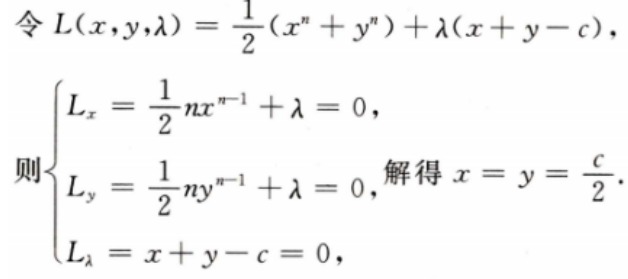
由实际问题的意义知当x=y=
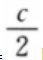时，f(x,y)取得最小值
