判断题
1、若
，则
。（）
答 案：错
解 析：
所以
单选题
1、已知f(x)的一个原函数为x2＋sinx，则
（）
答 案：C
解 析：由题意得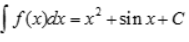
则
，
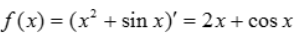所以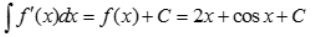
2、设函数f(x)在x=0处连续,g（x）在x = 0处不连续，则在x= 0处（）
答 案：D
解 析：f（x）在x=0处连续，g（x）在x=0处不连续，故f（x）＋g（x）在x=0处不连续，否则若f（x）＋g（x）在x=0处连续，则f（x）＋g（x）-f（x）=g（x）在x=0处连续，与题意矛盾，故选D选项.
主观题
1、若f（x）的一个原函数为xsinx,求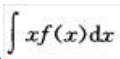
．
答 案：解：因为f（x）的一个原函数为xsinx，所以
因此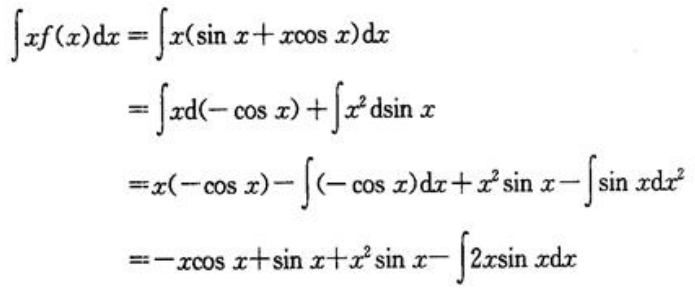
．
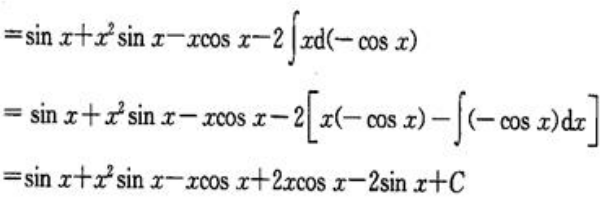
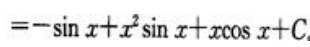2、求
．
答 案：解：
填空题
1、若随机变量x的期望与方差分别为1和9，则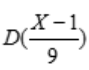
＝（）．
答 案：1/9
解 析：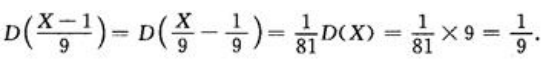
2、设z＝yx，则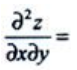
（）
答 案：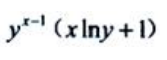
解 析：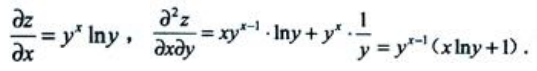
简答题
1、求曲线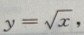
直线x=1和x轴所围成的有界平面图形的面积S，及该平面图形绕x轴旋转一周所得旋转体的体积V。
答 案：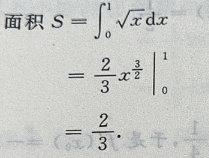
解 析：
2、设函数
求常数a。使f(x)在点x=0处连续。
答 案：
要f(x)在点x=0处连续，则需
所以a=1.
