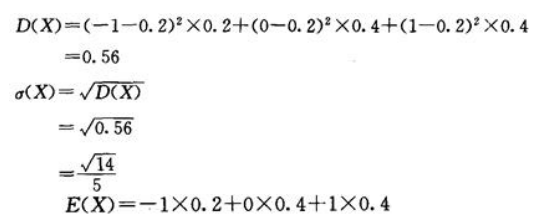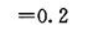判断题
1、若
，则
。（）
答 案：错
解 析：
所以
单选题
1、设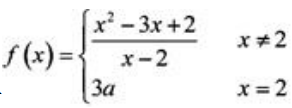
为连续函数，则a＝（）.
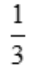
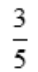
答 案：A
解 析：因为f(x)在x＝2连续，所以
故a＝.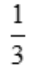
2、若x＝－1和x＝2都是函数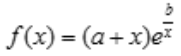
的极值点，则a，b分别为（）.
答 案：B
解 析：
由于x＝－1，x＝2是函数f(x)的极值点，则有
.即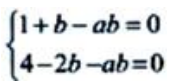
解得a＝2，b＝1.
主观题
1、证明：当x＞0时，
答 案：证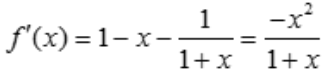：令
，
，令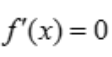
，得x＝0，f(0)=0，当x＞0时，f'(x)＜0，故函数单调递减，
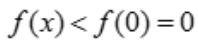，则
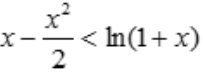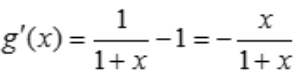．令
，
，令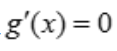
，得x＝0，g(0)=0，当x＞0时，f'(x)＜0，故函数单调递减，f(x)＜f(0)=0，则
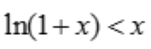．综上得，当x＞0时，
．
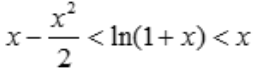2、甲袋中有15只乒乓球，其中3只白球，7只红球，5只黄球，乙袋中有20只乒乓球，其中10只白球，6只红球，4只黄球．现从两袋中各取一只球，求两球颜色相同的概率．
答 案：解：样本空间的样本点应该是甲、乙两袋中的样本点之积，也就是从甲袋中取一个球再从乙袋中取一球的所有取法，即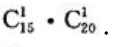
两球颜色相同的情况有三种，因此其样本点共有
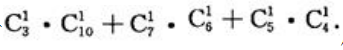所以两球颜色相同的概率为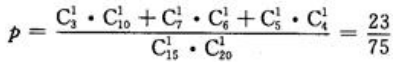
填空题
1、设事件A与B相互独立，且P(A)＝0.4，P(A＋B)＝0.7，则P(B)＝（）．
答 案：0.5
解 析：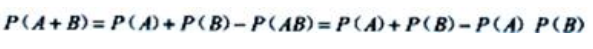
．即0.7＝0.4＋P(B)－0.4P(B)．得P(B)＝0.5．
2、设二元函数
，则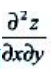
＝（）
答 案：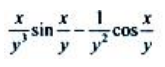
解 析：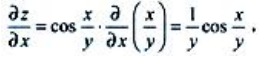
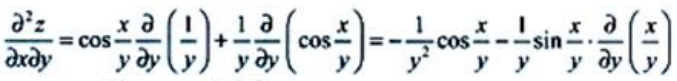
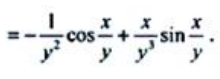
简答题
1、设D为由曲线y=x2，y=0，x=2所围成的图形. （1）求D的面积； （2）求D绕x轴旋转一周所得旋转体的体积.
答 案：（1）D的面积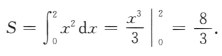
（2）D绕x轴旋转一周所得旋转体的体积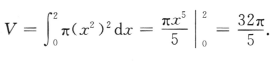
2、设随机变量X的概率分布为：
求X的期望、方差以及标准差．
答 案：
