单选题
1、级数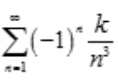
（k为非零常数）是（）的。
答 案：C
解 析：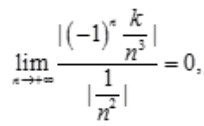
又
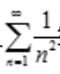绝对收敛，所以级数
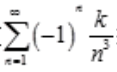绝对收敛。
2、在空间直角坐标系中方程y2＝x表示的是（）。
答 案：B
解 析：空间中，缺少一维坐标的方程均表示柱面，y2＝x是母线平行于z轴的柱面。
3、设函数f（x）在（0，1）内可导，f'（x）＞0，则f（x）在（0，1）内（）。
答 案：B
解 析：由于f'（x）＞0，可知，f（x）在（0，1）内单调增加。
主观题
1、求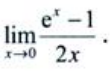
答 案：解：利用洛必达法则，得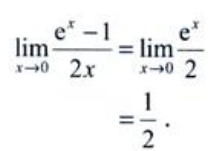
2、设z＝x2y—xy3，求
答 案：解：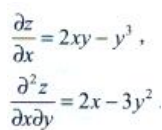
3、求过点M0（0，2，4），且与两个平面π1，π2都平行的直线方程，其中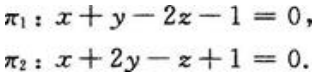
答 案：解：如果直线l平行于π1，则平面π1的法线向量n1必定垂直于直线l的方向向量s．同理，直线l平行于π2，则平面π2的法线向量n2必定满足n2⊥s．由向量积的定义可知，取
由于直线l过点M0（0，2，4），由直线的标准方程可知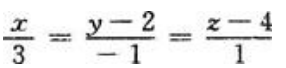
为所求直线方程。
填空题
1、曲线f(x)＝x3－x上点（1，0）处的切线方程为（）。
答 案：y＝2x－2
解 析：
，f'(1)＝2，故曲线在点（1，0）处的切线方程为y-0=2(x-1)，即y＝2x－2。
2、设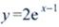
，则y＇＝（）。
答 案：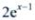
解 析：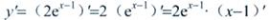
3、积分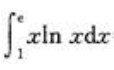
＝（）。
答 案：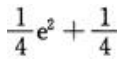
解 析：利用分部积分进行求解，得
简答题
1、讨论级数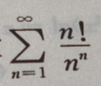
敛散性。
答 案：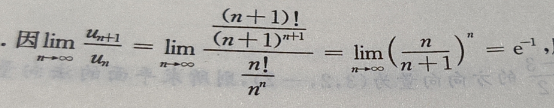
所以级数收敛。
