单选题

1、设函数f（x）＝sinx，则不定积分（）。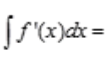

• A：sinx＋C
• B：cosx＋C
• C：-sinx＋C
• D：-cosx＋C

答 案：A

解 析：由不定积分性质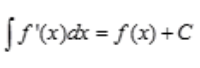

2、在空间直角坐标系中，方程x²＋z²＝z的图形是（）。

• A：圆柱面
• B：圆
• C：抛物线
• D：旋转抛物面

答 案：A

解 析：方程x²＋z²＝z可变形为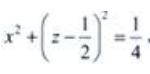，由此知该方程表示的是准线为圆、母线平行于y轴的圆柱面。

3、过点（1，0，0），（0，1，0），（0，0，1）的平面方程为（）。

• A：x＋y＋z＝1
• B：2x＋y＋z＝1
• C：x＋2y＋z＝1
• D：z＋y＋2z＝1

答 案：A

解 析：方法一：设所求平面方程为Ax＋By＋Cz＋D＝0.由于点（1，0，0），（0，1，0），（0，0，1）在平面上，将上述三点坐标分别代入所设方程，可得A＋D＝0，B＋D＝0，C＋D＝0，即A＝B＝C＝-D，再代回方程可得x＋y＋z＝1。方法二：由于点（1，0，0），（0，1，0），（0，0，1）分别位于x轴、y轴、z轴上，可由平面的截距式方程得出x＋y＋z＝1即为所求平面方程。

主观题

1、求y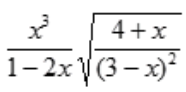＝的一阶导数y'。

答 案：解：两边取对数得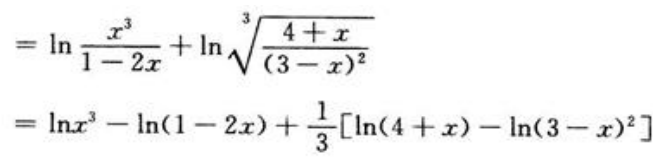两边对x求导得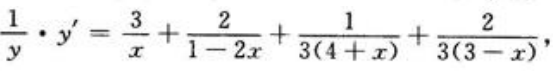故

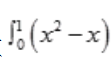2、计算dx。

答 案：解：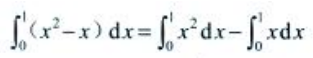

3、求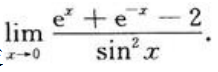

答 案：解：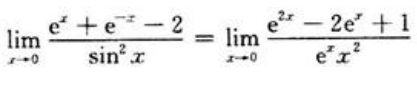

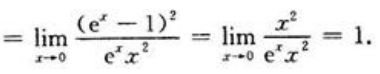
填空题

1、设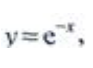则y''＝（）。

答 案：e^-x

解 析：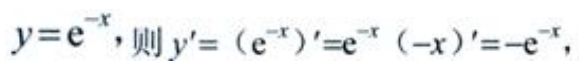

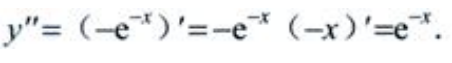
2、设D为（）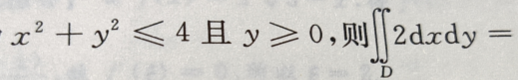

答 案：

解 析：因积分区域为圆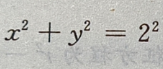的上半圆，则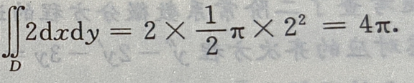

3、设z=xtan(y²+1)，则（）

答 案：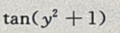

解 析：对x求偏导，可将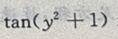看作是常数，故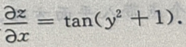

简答题

1、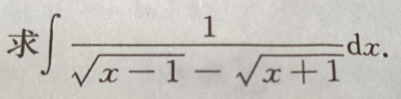

答 案：