判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
1、设函数f(x)=ln(3x),则f'(2)=().

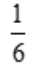
答 案:C
解 析: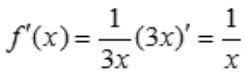 ,故
,故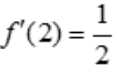 .
.
2、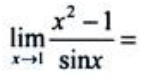 ().
().
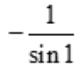
答 案:A
解 析: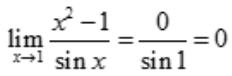 .
.
主观题
1、计算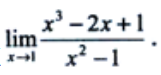
答 案:解:此处为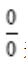 型极限,可使用洛必达法则
型极限,可使用洛必达法则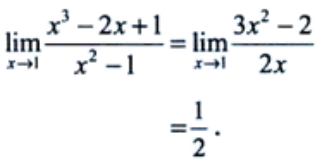
2、在半径为R的半圆内作一内接矩形,其中的一边在直径上,另外两个顶点在圆周上(如图所示).当矩形的长和宽各为多少时矩形面积最大?最大值是多少?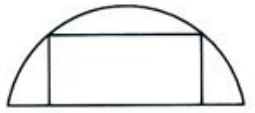
答 案:解:如图所示 ,设x轴通过半圆的直径,y轴垂直且平分直径.设OA=x,则AB=
,设x轴通过半圆的直径,y轴垂直且平分直径.设OA=x,则AB= ,矩形面积
,矩形面积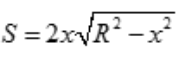 .
.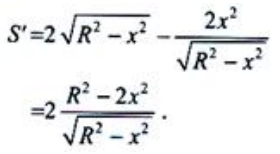 令s'=0,得
令s'=0,得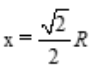 (舍去负值).
(舍去负值).
由于只有唯一驻点,根据实际问题x=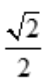 ,必为所求,则AB=
,必为所求,则AB=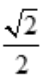 R.所以,当矩形的长为
R.所以,当矩形的长为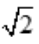 R、宽为
R、宽为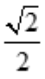 R时,矩形面积最大,且最大值S=R2.
R时,矩形面积最大,且最大值S=R2.
填空题
1、设f(x)是[-2,2]上的偶函数,且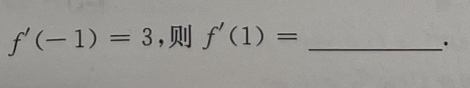
答 案:-3
解 析:因f(x)是偶函数,故 是奇函数,所以
是奇函数,所以 即
即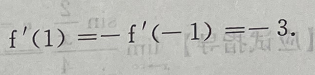
2、不定积分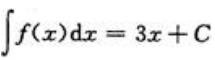 ,则
,则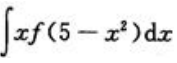 =().
=().
答 案: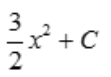
解 析: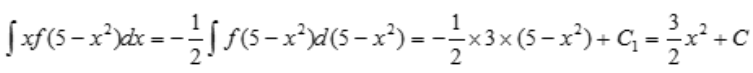 .
.
简答题
1、试确定a,b的值,使函数f(x)=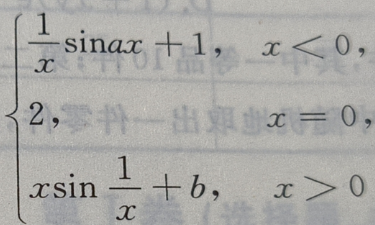 在点x=0处连续。
在点x=0处连续。
答 案: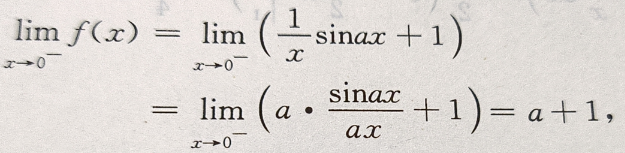
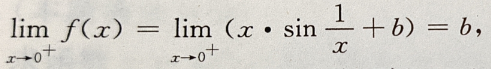 因为f(x)在x=0处连续,则
因为f(x)在x=0处连续,则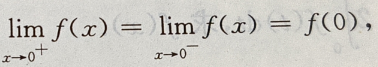 即a+1=b=2,即a=1,b=2.
即a+1=b=2,即a=1,b=2.
2、设函数 求常数a。使f(x)在点x=0处连续。
求常数a。使f(x)在点x=0处连续。
答 案: 要f(x)在点x=0处连续,则需
要f(x)在点x=0处连续,则需 所以a=1.
所以a=1.