单选题
1、设y(n-2)=sinx,则y(n)=()
答 案:D
解 析: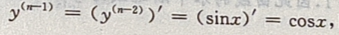 因此
因此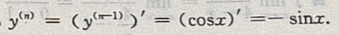
2、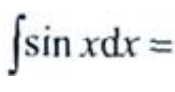 ()。
()。
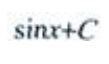
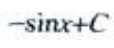
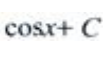

答 案:D
解 析:由不定积分的基本积分公式可得,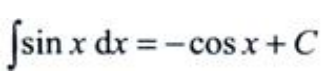 。
。
3、已知f(xy,x-y)=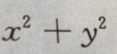 则
则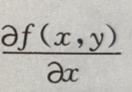 等于()
等于()
答 案:A
解 析:因f(xy,x-y)=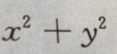 =
=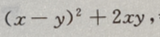 故
故 从而
从而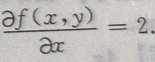
主观题
1、设f(x)是以T为周期的连续函数,a为任意常数,证明: 。
。
答 案:证:因为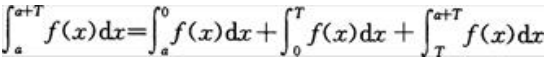 令x=T+t,做变量替换得
令x=T+t,做变量替换得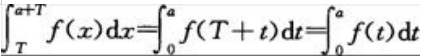 故
故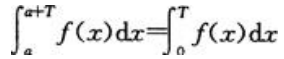
2、求微分方程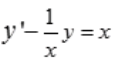 的通解。
的通解。
答 案:解: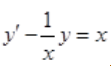 为一阶线性微分方程,则
为一阶线性微分方程,则
3、求微分方程 的通解.
的通解.
答 案:解:对应齐次微分方程的特征方程为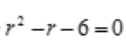 ,解得r1=3,r2=-2.所以齐次通解为
,解得r1=3,r2=-2.所以齐次通解为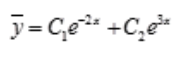 。设方程的特解设为y*=(Ax+B)ex,代入原微分方程可解得,A=
。设方程的特解设为y*=(Ax+B)ex,代入原微分方程可解得,A=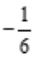 ,B=
,B=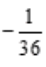 .即非齐次微分方程特解为
.即非齐次微分方程特解为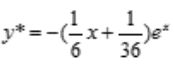 。所以微分方程
。所以微分方程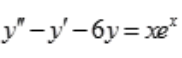 的通解为
的通解为 。
。
填空题
1、函数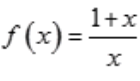 在[1,2]上符合拉格朗日中值定理的
在[1,2]上符合拉格朗日中值定理的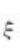 =_。
=_。
答 案:
解 析:由拉格朗日中值定理有 解得
解得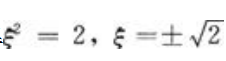 ,其中
,其中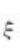 =-
=- (舍),得
(舍),得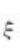 =
= 。
。
2、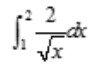 =()。
=()。
答 案: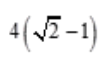
解 析: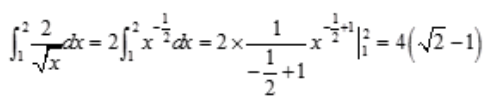 。
。
3、 =()。
=()。
答 案:
解 析:所给求极限的表达式为分式,x=1时分母不为零,可将x=1直接代入函数求得极限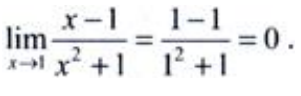
简答题
1、求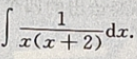
答 案: