单选题
1、下列函数中，为奇函数的是（）
- A：
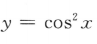
- B：
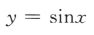
- C：
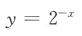
- D：
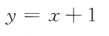
答 案：B
解 析：当f(-x)＝-f(x)，函数f(x)是奇函数，只有选项B符合.
2、在△ABC中，若lgsinA-lgsinB-lgcos=lg2，则△ABC是（）
- A：以A为直角的三角形
- B：b=c的等腰三角形
- C：等边三角形
- D：钝角三角形
答 案：B
解 析：判断三角形的形状，条件是用一个对数等式给出先将对数式利用对数的运算法则整理。 ∵lgsinA-lgsinB-lgcos=lg2，由对数运算法则可得,左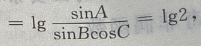
两个对数底数相等则真数相等：
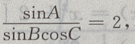即2sinBcosC=sinA
在△ABC中，∵A+B+C=180°，∴A=180°-（B+C）,
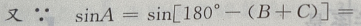
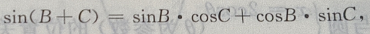
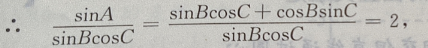
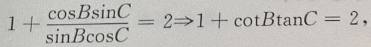
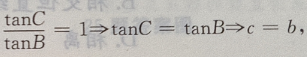故为等腰三角形
3、从点M(x,3)向圆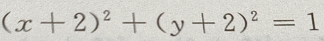
作切线，切线的最小值等于（）
- A：4
- B：
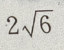
- C：5
- D：
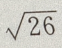
答 案：B
解 析：如图,相切是直线与圆的位置关系中的一种，此题利用圆心坐标、半径，求出切线长. 由圆的方程知,圆心为B(-2,-2),半径为1，设切点为A，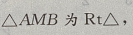
由勾股定理得，
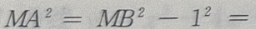
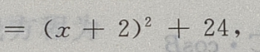
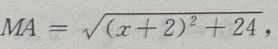当x+2=0时，MA取最小值，最小值为
4、设集合A={0,1}，B={0,1,2}，则A∩B=（）
- A：{1,2}
- B：{0,2}
- C：{0,1}
- D：{0,1,2}
答 案：C
解 析：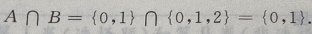
主观题
1、设函数f(x)=
(Ⅰ)求f(x)的单调区间;
(Ⅱ)求 f(x)的极值
答 案：(Ⅰ)函数的定义域为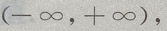
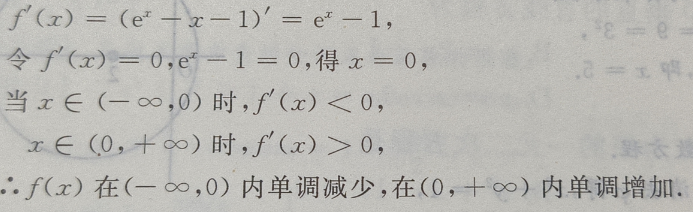(Ⅱ)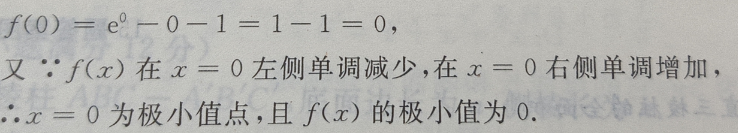
2、设函数f(x)=xlnx+x.(I）求曲线y=f(x）在点（(1,f(1))处的切线方程；
(II）求f（x）的极值．
答 案：(I）f(1)=1,f'(x)=2+lnx，故f'(1)=2.所以曲线y=f(x）在点（1,f(1))处的切线方程为y=2x-1.(II）令f'(x)=0，解得
当
时，f'(x)
单调递减，在区间
单调递增．因此f(x）在
时取得极小值
3、在正四棱柱ABCD-A'B'C'D'中，
（Ⅰ）写出向量
和
关于基底{a,b,c}的分解式;
（Ⅱ）求证：
（Ⅲ）求证：
答 案：（Ⅰ）由题意知(如图所示)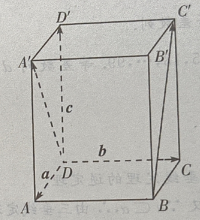 
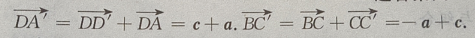
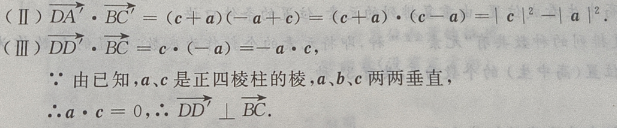
4、在正四棱柱ABCD-A'B'C'D'中，
（Ⅰ）写出向量
关于基底{a,b,c}的分解式
（Ⅱ）求证：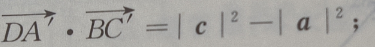
（Ⅲ）求证：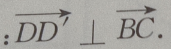
答 案：(Ⅰ)由题意知(如图所示)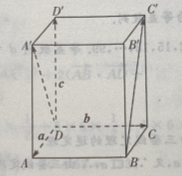 
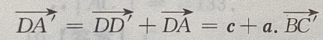
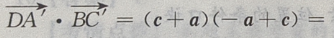
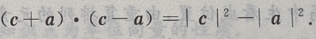(Ⅱ)
(Ⅲ)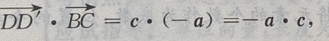
由已知，a,c是正四棱柱的棱，a,b,c两两垂直
填空题
1、椭圆的中心在原点，一个顶点和一个焦点分别是直线x+3y-6与两坐标轴的交点,则此椭圆的标准方程为（）
答 案：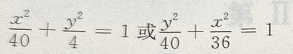
解 析：原直线方程可化为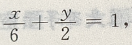
交点(6,0),(0,2). 当点(6,0)是椭圆一个焦点,点(0,2) 是椭圆一个顶点时,c=6,b=2,
当点(0,2) 是椭圆一个焦点,(6,0) 是椭圆一个顶点时,c=2,b-6,
2、不等式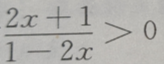
的解集为（）
答 案：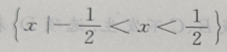
解 析：
