判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
1、下列变量在给定的变化过程中是无穷小量的是()



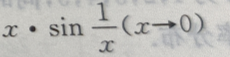
答 案:D
解 析:由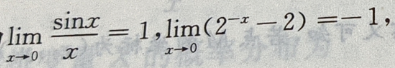 故由无穷小量知应选D,
故由无穷小量知应选D,
2、设f'(x)在-闭区间[0,1]上连续,则曲线y=f(x)与直线x=0,x=1和y=0所围成的平面图形的面积等于()
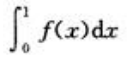
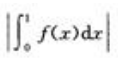
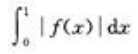
答 案:C
解 析:由定积分的几何意义可知,当在区间[a,b]上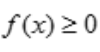 时,
时,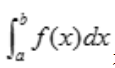 表示曲线y=f(x)与两条直线x=a,x=b以及x轴所围成的曲边梯形的面积;当在区间[a,b]上
表示曲线y=f(x)与两条直线x=a,x=b以及x轴所围成的曲边梯形的面积;当在区间[a,b]上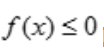 时,
时,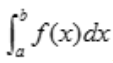 表示曲线y=f(x)与两条直线x=a,x=b以及x轴所围成的曲边梯形面积的负值
表示曲线y=f(x)与两条直线x=a,x=b以及x轴所围成的曲边梯形面积的负值
主观题
1、袋中有10个乒乓球.其中6个白球、4个黄球,随机地抽取两次,每次取1个,不放回.设A={第一次取到白球),B={第二次取到白球},求P(B|A).
答 案:解:因为样本空间的基本事件有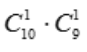 个.而AB表示第一次取白球且第二次也取白球,故引起事件AB的基本事件有
个.而AB表示第一次取白球且第二次也取白球,故引起事件AB的基本事件有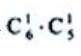 个,所以
个,所以 而
而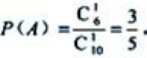 ;所以
;所以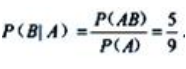 ;
;
2、设事件A与B相互独立,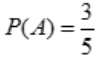 ,
,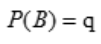 ,
,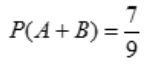 ,求q.
,求q.
答 案:解:因为事件A与B相互独立,故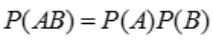 ,
, ,即
,即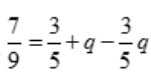 ,解得
,解得 =
=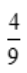 .
.
填空题
1、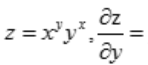 ()
()
答 案:
解 析: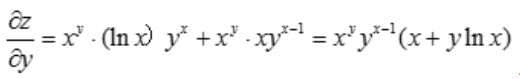
2、已知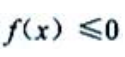 ,且f(x)在[a,b]连续,则由曲线y=f(x),x=a、x=b及x轴围成的平面图形的面积A=().
,且f(x)在[a,b]连续,则由曲线y=f(x),x=a、x=b及x轴围成的平面图形的面积A=().
答 案: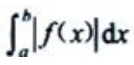
解 析: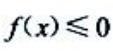 ,则有
,则有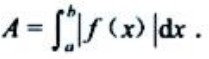
简答题
1、求函数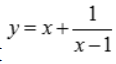 的单调区间、极值及凹凸区间.
的单调区间、极值及凹凸区间.
答 案:函数定义域为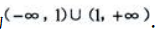 求导得
求导得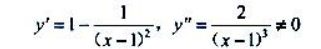 令
令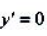 得
得 列表得
列表得 函数
函数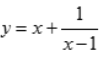 的单调增加区间为
的单调增加区间为 单调减少区间为
单调减少区间为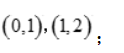
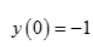 为极大值,
为极大值, 极小值;凸区间为
极小值;凸区间为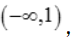 凹区间为
凹区间为 。
。
2、已知函数f(x)=ax3-bx2+cx在区间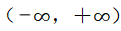 内是奇函数,且当x=1时,f(x)有极小值
内是奇函数,且当x=1时,f(x)有极小值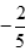 ,求另一个极值及此曲线的拐点.
,求另一个极值及此曲线的拐点.
答 案:f(x)=ax3-bx2+cx,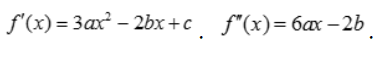 由于f(x)是奇函数,则必有x2的系数为0,即b=0.
由于f(x)是奇函数,则必有x2的系数为0,即b=0.
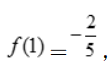 即a+c=
即a+c=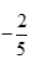 ,
,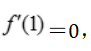 得3a+c=0.解得a=
得3a+c=0.解得a=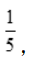 c=
c= 此时
此时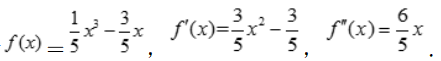 令
令 得
得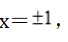
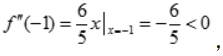 所以
所以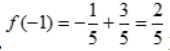 为极大值,
为极大值,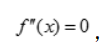 得x=0,x<0时,
得x=0,x<0时,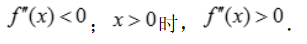 所以(0,0)为曲线的拐点.
所以(0,0)为曲线的拐点.