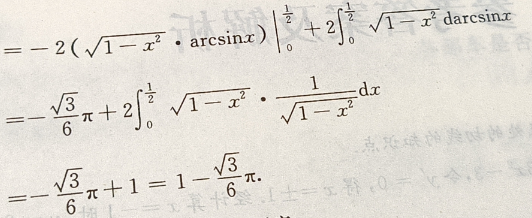判断题
1、若
，则
。（）
答 案：错
解 析：
所以
单选题
1、设A，B是两随机事件，则事件A－B表示（）.
答 案：C
解 析：事件A－B表示事件A发生而事件B不发生.
2、设函数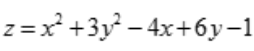
，则驻点坐标为（）.
答 案：A
解 析：令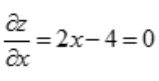
与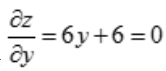
，可得ｘ＝２，ｙ＝－１，故驻点为（2，-1）.
主观题
1、求函数f(x,y)＝x2＋y2在条件2x＋3y＝1下的极值．
答 案：解：求条件极值，作拉普拉斯辅助函数F（x，y，λ）＝f(x,y)＋λ（2x＋3y－1）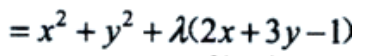
令
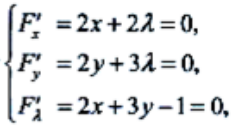得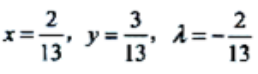
．
因此，f(x,y)在条件2x＋3y＝1下的极值为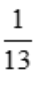
．
2、当
．
答 案：证：设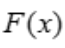
＝ex－x－1，
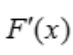＝ex－1．当x＜0时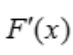，＜0，F（x）单调递减，所以当x＜0时，F（x）＞F（0）＝0，即ex－x－1＞0，得ex＞1＋x．
填空题
1、函数z＝2（x－y）－x2－y2的驻点坐标为（）．
答 案：（1，－1）
解 析：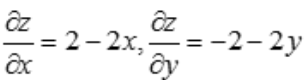
，令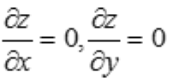
，得x=1,y=-1，则函数的驻点坐标为（1，－1）．
2、己知y＝x3-ax在x＝1的切线平行于直线5x-ｙ+1＝0，则ａ＝（）
答 案：-2
解 析：
a=-2
简答题
1、设函数
求常数a。使f(x)在点x=0处连续。
答 案：
要f(x)在点x=0处连续，则需
所以a=1.
2、计算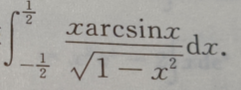
答 案：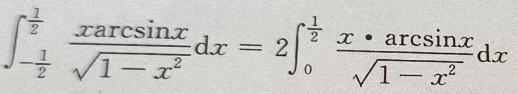
（被积函数为偶函数）
