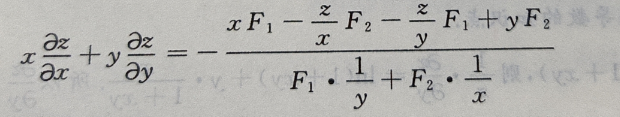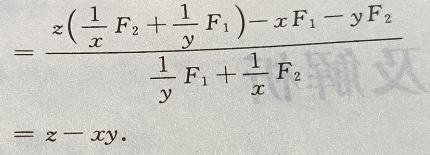单选题
1、曲线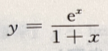
答 案:D
解 析:因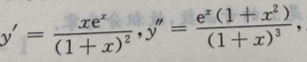 则
则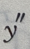 在定义域内恒不等于0,所以无拐点。
在定义域内恒不等于0,所以无拐点。
2、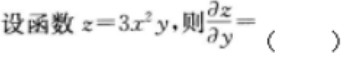
答 案:D
3、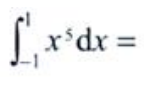 ()。
()。
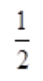
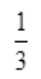
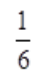
答 案:D
解 析:被积函数x5为奇函数,积分区间[1,1]为对称区间,由定积分对称性质可知 。
。
主观题
1、求微分方程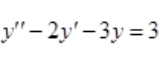 的通解.
的通解.
答 案:解:原方程对应的齐次微分方程为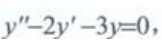 特征方程为
特征方程为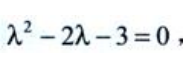 特征根为x1=-1,x2=3,
特征根为x1=-1,x2=3,
齐次方程的通解为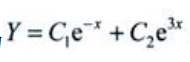
设原方程的特解为 =A,代入原方程可得
=A,代入原方程可得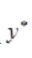 =-1。
=-1。
所以原方程的通解为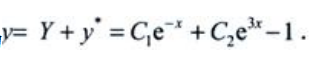 (C1,C2为任意常数)
(C1,C2为任意常数)
2、计算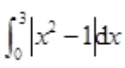 。
。
答 案:解:
3、求函数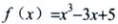 的极大值与极小值。
的极大值与极小值。
答 案:解: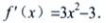 令f′(x)=0,解得x1=-1;x2=1又f″(x)=6x,可知f″(-1)=-6<0,f″(1)=6>0
令f′(x)=0,解得x1=-1;x2=1又f″(x)=6x,可知f″(-1)=-6<0,f″(1)=6>0
故x=-1为f(x)的极大值点,极大值为7
x=1为f(x)的极小值点,极小值为3。
填空题
1、曲线y=x3+2x+3的拐点坐标是()。
答 案:(0,3)
解 析:y=x3+2x+3,y'=3x2+2,y''=6x.令y''=0,得x=0.当x=0时,y=3。当x<0时,y''<0;当x>0时,y''>0.因此(0,3)为曲线的拐点。
2、微分方程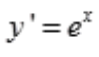 的通解是()。
的通解是()。
答 案:y=ex+C
解 析: ,分离变量,得dy=exdx,两边积分得y=ex+C,即为通解。
,分离变量,得dy=exdx,两边积分得y=ex+C,即为通解。
3、通解为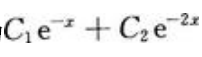 的二阶常系数线性齐次微分方程是()。
的二阶常系数线性齐次微分方程是()。
答 案: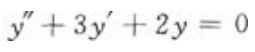
解 析:特征方程的两根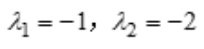 ,故特征方程为
,故特征方程为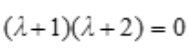 ,即
,即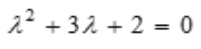 ,则二阶常系数线性齐次微分方程
,则二阶常系数线性齐次微分方程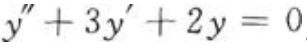 。
。
简答题
1、设函数z(x,y)由方程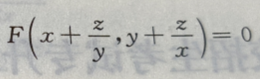 所确定
证明:
所确定
证明: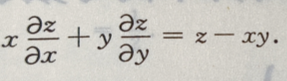
答 案: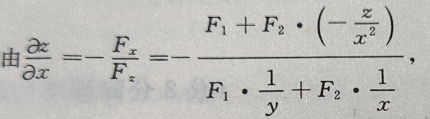
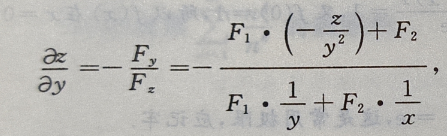 所以
所以