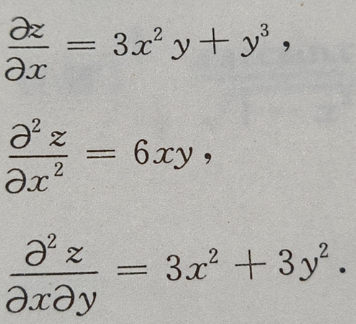判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
1、设函数z=ln(x+y),则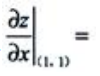 ().
().
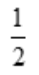
答 案:B
解 析: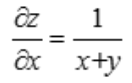 ,
,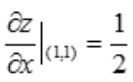 .
.
2、下列说法正确的是().
答 案:C
解 析:函数在某点连续,但是不一定可导或可微,例如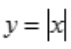 在x=0处连续,但是不可导也不可微.如果函数在某点可导,则函数在此点的导数一定存在,所以在此点一定连续.
在x=0处连续,但是不可导也不可微.如果函数在某点可导,则函数在此点的导数一定存在,所以在此点一定连续.
主观题
1、计算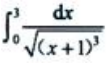 .
.
答 案:解: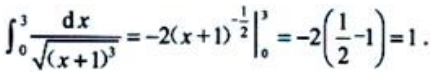
2、求二元函数 的极值.
的极值.
答 案:解:令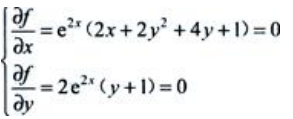 解得驻点
解得驻点 A=
A=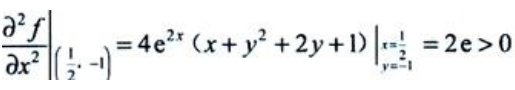 ,
, ,
,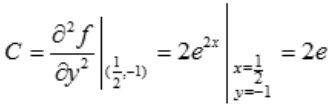 ,
, ,且A>0.所以在点
,且A>0.所以在点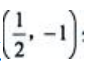 处函数f(x,y)取极小值,极小值为
处函数f(x,y)取极小值,极小值为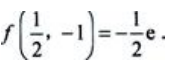
填空题
1、设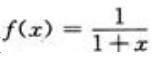 ,f(x0)=5,则
,f(x0)=5,则 =().
=().
答 案:
解 析:因为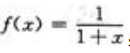 ,f(x0)=5,所以
,f(x0)=5,所以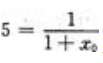 ,即
,即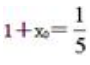 ,所以
,所以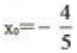 ;因为
;因为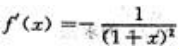 所以
所以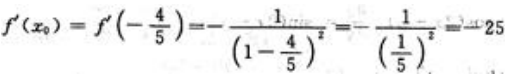 ,即
,即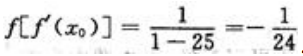 .
.
2、 ()
()
答 案:
解 析: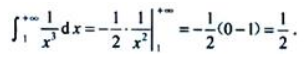
简答题
1、计算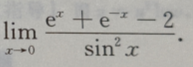
答 案: ps:将分母
ps:将分母 用于之等价的无穷小量
用于之等价的无穷小量 代换,这是一个技巧。
代换,这是一个技巧。
2、设函数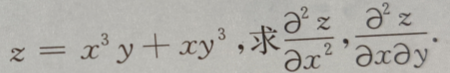
答 案: