单选题
1、下列级数中绝对收敛的是()。
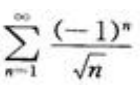
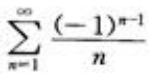
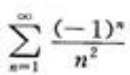

答 案:C
解 析:本题考查绝对收敛的定义.A项,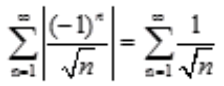 发散;B项,
发散;B项, 发散,即
发散,即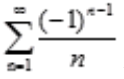 条件收敛;C项,
条件收敛;C项, 收敛;D项,
收敛;D项,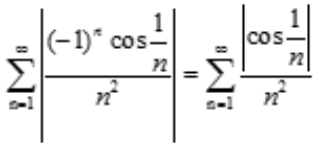 发散。
发散。
2、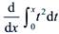 =()。
=()。
答 案:A
解 析:由可变限积分求导公式可知 。
。
3、设函数f(x)在(0,1)上可导且在[0,1]上连续,且f'(x)>0,f(0)<0,f(1)>0,则f(x)在(0,1)内()。
答 案:B
解 析:因为函数f(x)在[0,1]上连续,f(0)<0,f(1)>0,故存在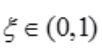 ,使得
,使得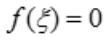 ,又f'(x)>0,函数在(0,1)上单调增加,故f(x)在(0,1)内有且仅有一个零点。
,又f'(x)>0,函数在(0,1)上单调增加,故f(x)在(0,1)内有且仅有一个零点。
主观题
1、设y=㏑x,求y(n)。
答 案:解: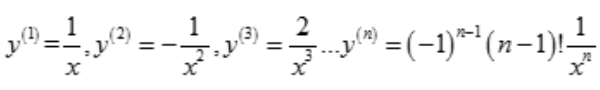 。
。
2、计算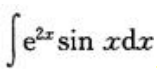 .
.
答 案:解: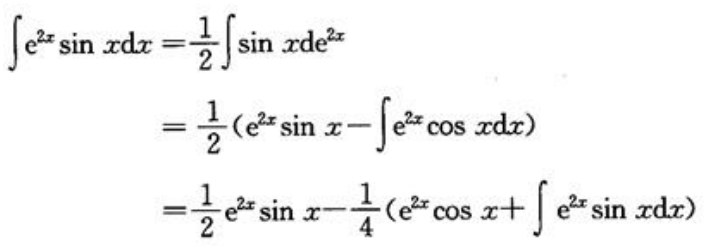 从而有
从而有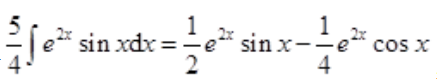 ,所以
,所以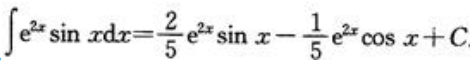
3、在曲线 上求一点M0,使得如图中阴影部分的面积S1与S2之和S最小。
上求一点M0,使得如图中阴影部分的面积S1与S2之和S最小。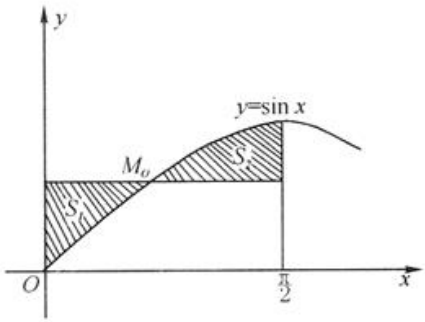
答 案:解:设点M0的横坐标为x0,则有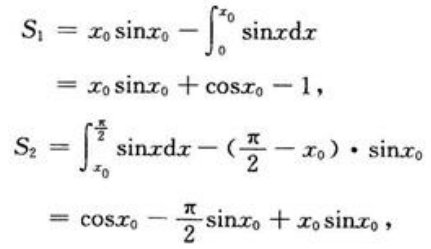 则
则 S为x0的函数,将上式对x0求导得
S为x0的函数,将上式对x0求导得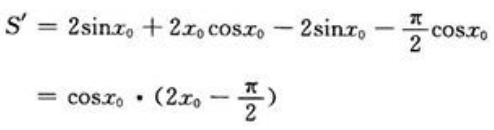 令S'=0,得
令S'=0,得 ,所以
,所以 由于只有唯一的驻点,所以
由于只有唯一的驻点,所以 则点M0的坐标为
则点M0的坐标为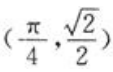 为所求。
为所求。
填空题
1、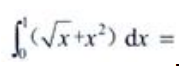 ()。
()。
答 案:1
解 析: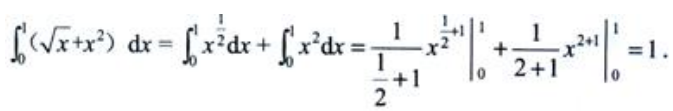
2、设a≠0,则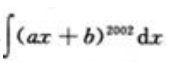 =()。
=()。
答 案: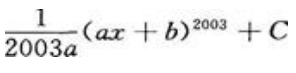
解 析: 。
。
3、函数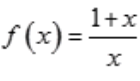 在[1,2]上符合拉格朗日中值定理的
在[1,2]上符合拉格朗日中值定理的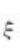 =_。
=_。
答 案:
解 析:由拉格朗日中值定理有 解得
解得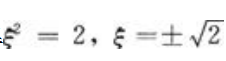 ,其中
,其中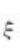 =-
=- (舍),得
(舍),得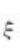 =
= 。
。
简答题
1、设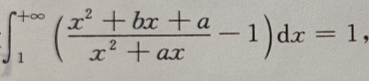 求常数a,b
求常数a,b
答 案: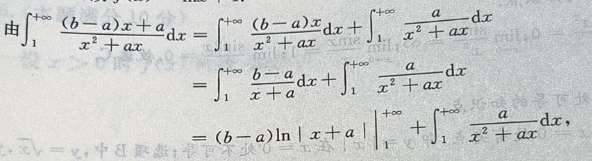 由此积分收敛知,应有b-a=0,即b=a,
由此积分收敛知,应有b-a=0,即b=a,