判断题

1、若，则。（）  

答 案：错

解 析：所以  

单选题

1、设函数f(x)＝cosx，则＝（）.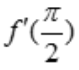

• A：－1
• B：
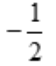
• C：0
• D：1

答 案：A

解 析：，.

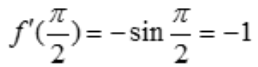2、（ ）．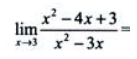  

• A：0
• B：1
• C：
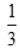
• D：

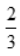
答 案：D

解 析：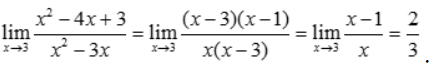

主观题

1、5人排成一行，试求下列事件的概率：（1）A＝{甲、乙二人必须排在头尾}
（2）B＝{甲、乙二人必须间隔一人排列}

答 案：解：5人排成1行的所有排法为5！．（1）甲、乙2人必须排在头尾的排法是2！，其余3人只能排在中间的排法是3！，所以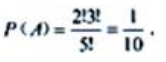（2）甲、乙2人必须间隔一人排列，则甲、乙之间可以间隔其他三人中任意一个，甲、乙之间可以调换次序，共有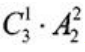种方法．将三人视为整体，与其他两人排列有种方法．所以

2、己知某篮球运动员每次投篮投中的概率是0.9，记X为他两次独立投篮投中的次数．（1）求X的概率分布；
（2）求X的数学期望EX．

答 案：解：（1）X可能的取值为0，1，2；因此X的概率分布为 （2）数学期望
EX＝0×0.1＋1×0.18＋2×0.81＝1.80

填空题

1、设函数z＝x²＋lny，则dz＝（）．

答 案：2xdx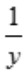＋dy

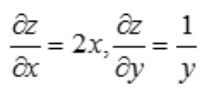解 析：，故．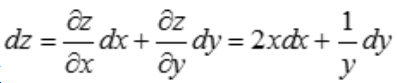

2、斜边长为l的直角三角形中，最大周长为（）

答 案：（1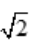＋）l

解 析：该题也是条件极值问题，用拉格朗日乘数法求解，设直角三角形的两直角边长分别为x和y，周长为z，且z＝l＋x＋y（0＜x＜l，0＜y＜l），条件函数为l²＝x²＋y².令F（x，y，λ）＝l＋x＋y＋λ（x²＋y²－l²）求解方程组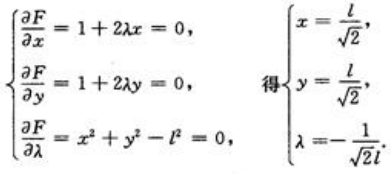根据实际意义，一定存在最大周长，所x＝y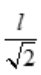＝时，即斜边长为l时的等腰直角三角形周长最大，且此周长为（1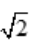＋）l.

简答题

1、求曲线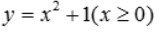与y＝x＋1所围成的图形分别绕x轴和y轴旋转所得旋转体的体积．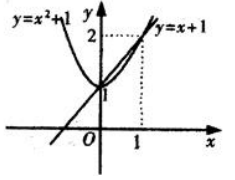

答 案：（1）绕x轴旋转的体积为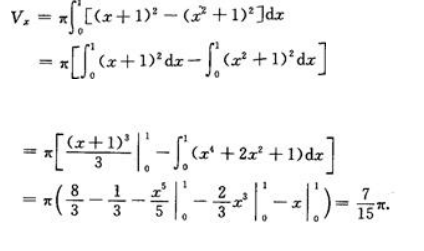 （2）绕y轴旋转的体积为

2、计算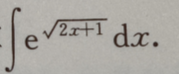

答 案：