2024年成考专升本《高等数学一》每日一练试题03月05日
精选习题
2024-03-05
11:30:16
收藏
单选题
1、设 ,则y'=()。
,则y'=()。
- A:2x
- B:3+2x
- C:3
- D:x2
答 案:A
解 析: 。
。
2、设x是f(x)的一个原函数,则f(x)=()。
- A:
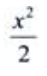
- B:
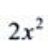
- C:1
- D:C(任意常数)
答 案:C
解 析:x为f(x)的一个原函数,则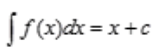 ,等式两边同时求导,得
,等式两边同时求导,得 。
。
3、已知f(xy,x-y)=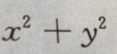 则
则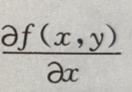 等于()
等于()
- A:2
- B:2x
- C:2y
- D:2x+2y
答 案:A
解 析:因f(xy,x-y)=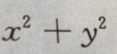 =
=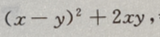 故
故 从而
从而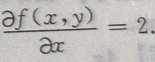
主观题
1、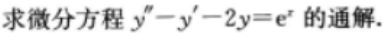
答 案:
2、求微分方程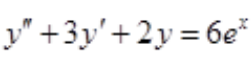 的通解.
的通解.
答 案:解:原方程对应的齐次方程为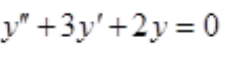 。特征方程为,r2+3r+2=0,特征值为r1=-2,r2=-1。齐次方程的通解为y=C1e-2x+C2e-x。
。特征方程为,r2+3r+2=0,特征值为r1=-2,r2=-1。齐次方程的通解为y=C1e-2x+C2e-x。
设特解为y*=Aex,代入原方程有6A=6,得A=1。
所以原方程的通解为y=C1e-2x+C2e-X+ex(C1,C2为任意常数)。
3、求y'+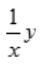 =1的通解.
=1的通解.
答 案:解:
填空题
1、设区域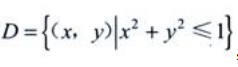 ,则
,则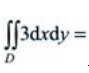 ()。
()。
答 案:3π
解 析:积分区域D为半径为1的圆域,其面积为π,因此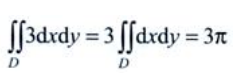 。
。
2、曲线f(x)=x3-x上点(1,0)处的切线方程为()。
答 案:y=2x-2
解 析: ,f'(1)=2,故曲线在点(1,0)处的切线方程为y-0=2(x-1),即y=2x-2。
,f'(1)=2,故曲线在点(1,0)处的切线方程为y-0=2(x-1),即y=2x-2。
3、过点(1,0,-1)与平面3x-y-z-2=0平行的平面的方程为()
答 案:3x-y-z-4=0
解 析:平面3x-y-z-2=0的法向量为(3,-1,-1),所求平面与其平行,故所求的平面的法向量为(3,-1,-1),由平面的点法式方程得所求平面方程为3(x-1)-(y-0)-(z+1)=0,及3x-y-z-4=0。
简答题
1、证明:当x>0时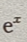 >1+x.
>1+x.
答 案: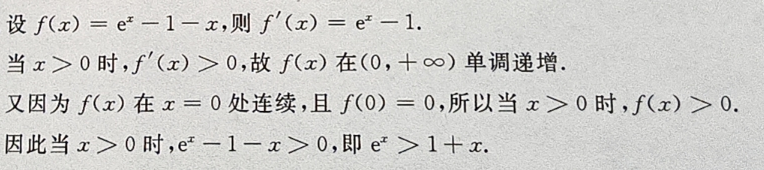
更多推荐

