判断题
1、若
，则
。（）
答 案：错
解 析：
所以
单选题
1、设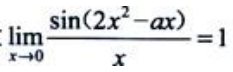
,则a＝（）.
答 案：A
解 析：
，所以a＝-1.
2、以下结论正确的是（）.
答 案：C
解 析：A项，函数f(x)的极值点不一定是可导点；B项，驻点是导数为零的点，不一定是极值点，比如当f(x)＝x3时，x＝0为其驻点，但不是其极值点；D项，连续不一定可导.
主观题
1、计算
答 案：解：
2、已知函数f(x)＝－x2＋2x．（1）求曲线y＝f(x)与x轴所围成的平面图形的面积S；
（2）求（1）中的平面图形绕x轴旋转一周所得旋转体的体积V．
答 案：解：（1）由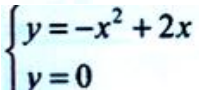
得曲线与x轴交点坐标为（0，0），（2，0）．
（2）
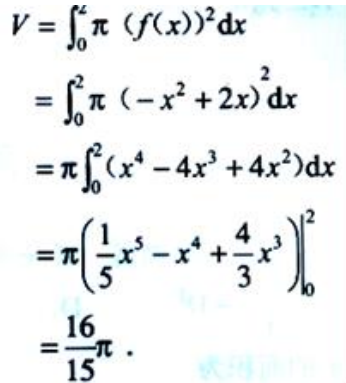
填空题
1、设函数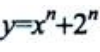
，则
＝（）．
答 案：n!
解 析：先求出函数的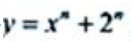
的n阶导数，再将x＝1代入，注意：2n是常数项．因为
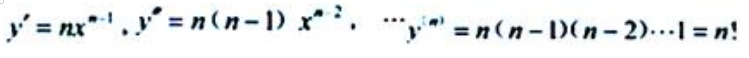所以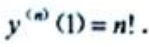
2、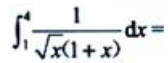
()．
答 案：2arctan2－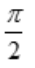
解 析：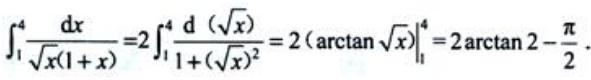
简答题
1、从一批有10件正品及2件次品的产品中，不放回地一件一件地抽取产品．设每个产品被抽到的可能性相同。求直到取出正品为止所需抽取的次数X的概率分布。
答 案：
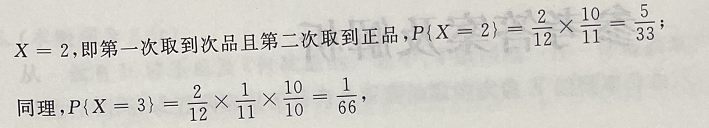
2、求曲线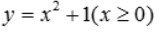
与y＝x＋1所围成的图形分别绕x轴和y轴旋转所得旋转体的体积．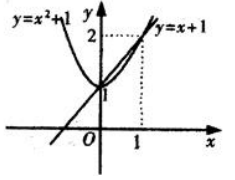
答 案：（1）绕x轴旋转的体积为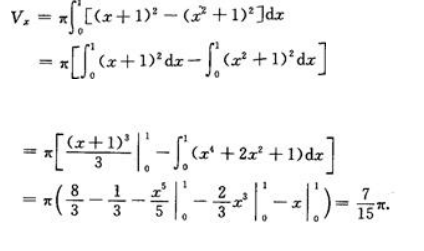
（2）绕y轴旋转的体积为
