判断题
1、若
，则
。（）
答 案：错
解 析：
所以
单选题
1、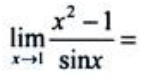
（）.
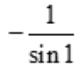
答 案：A
解 析：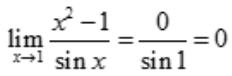
.
2、设函数y＝ex－ln3，则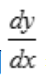
＝（）.
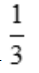
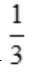
答 案：A
解 析：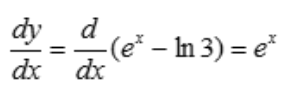
.
主观题
1、求二元函数f(x,y)＝x2＋y2＋2y的极值．
答 案：解：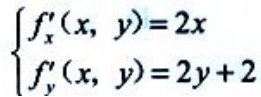
，令
，得驻点（0,－1）．因为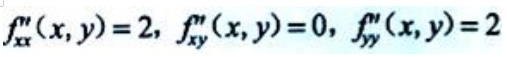
所以
由于A＞0且
，故f（x，y）在点（0，1）处取得极小值，极小值为f（0，－1）＝－1．
2、求函数f(x)＝
的单调区间、极值和曲线y＝f(x)的凹凸区间．
答 案：解：函数的定义域为（－∞，＋∞）．求导得y'＝x2－4，y''＝2x令y'＝0，得x＝±2．y''＝0，得x＝0．
函数f(x)的单调增区间为（－∞，－2），（2，＋∞），函数f(x)的单调减区间为（－2，2）；
函数的极大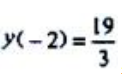值为
，极小值为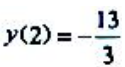
；
曲线的凸区间为（－∞，0），曲线的凹区间为（0，＋∞）．
填空题
1、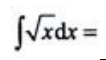
（）．
答 案：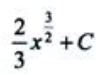
解 析：由积分公式得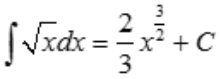
．
2、设A，B为两个随机事件，且P（A）=0.5，P（AB）=0.4，则P（B|A）=（）
答 案：0.8
解 析：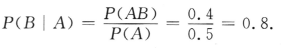
简答题
1、求曲线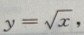
直线x=1和x轴所围成的有界平面图形的面积S，及该平面图形绕x轴旋转一周所得旋转体的体积V。
答 案：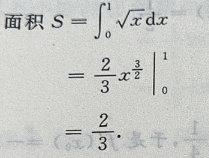
解 析：
2、计算
答 案：由洛必达法则有
