2024年成考专升本《高等数学一》每日一练试题02月18日
精选习题
2024-02-18
11:29:36
收藏
单选题
1、设z=arcsinx+ey,则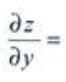 ()。
()。
- A:
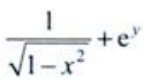
- B:

- C:
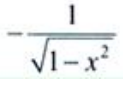
- D:ey
答 案:D
解 析:求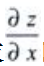 时,将x看作常量,z=arcsinx+ey,因此
时,将x看作常量,z=arcsinx+ey,因此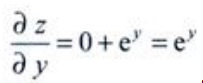 。
。
2、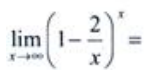 ()。
()。
- A:
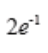
- B:
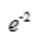
- C:
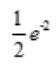
- D:
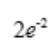
答 案:B
解 析:根据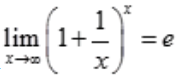 ,可得
,可得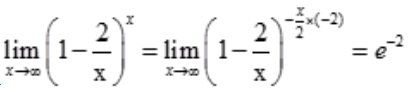 。
。
3、下列等式成立的是()
- A:
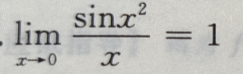
- B:
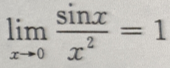
- C:
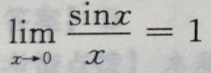
- D:
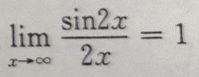
答 案:C
解 析:由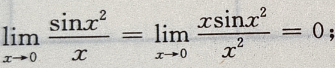
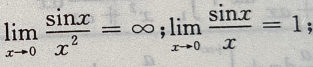
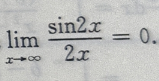
主观题
1、设y=㏑x,求y(n)。
答 案:解: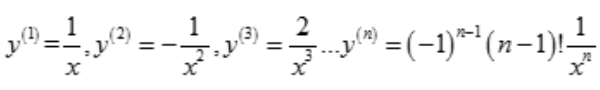 。
。
2、求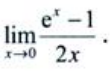
答 案:解:利用洛必达法则,得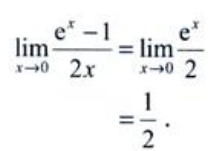
3、计算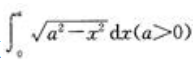 。
。
答 案:解:令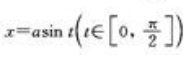 ,
,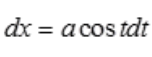 ,则
,则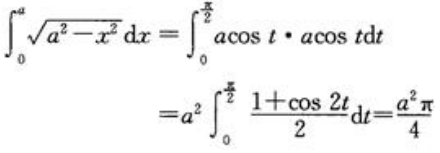
填空题
1、直线 的标准式方程为()。
的标准式方程为()。
答 案:
解 析:取z=0,可得直线上一点(-5,-8,0)直线的方向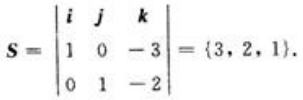 所以直线方程为:
所以直线方程为:
2、 =()。
=()。
答 案:
解 析:所给求极限的表达式为分式,x=1时分母不为零,可将x=1直接代入函数求得极限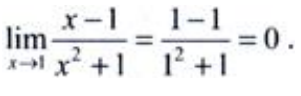
3、极限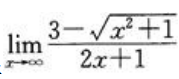 =()。
=()。
答 案: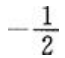
解 析: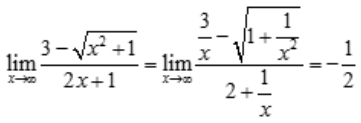 。
。
简答题
1、计算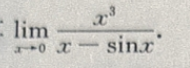
答 案: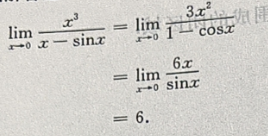
更多推荐

