判断题
1、—组数据8,8,7,10,6,8,9的众数和中位数都是8。()
答 案:对
解 析:在这组数据中,8出现了3次,出现的次数最多,则众数是8,把这组数据从小到大排列,最中间的数是8;则这组数据中众数和中位数都是8,正确。
2、已知a,b,c,d为实数,a>b且c>d,则a-c>b-d()
答 案:错
解 析:用特殊值法,令a=2,b=-2,c=1,d=-4,代入a-c=1,b-d=2,a-c
单选题
1、若函数 ,且f(1)=f(3),则f(-1)=()
,且f(1)=f(3),则f(-1)=()
答 案:D
解 析:由题意得x=1和3是x2+bx+c=0的解
所以-b=1+3=4,b=-4
c=1×3=3
f(x)=x2+bx+c=x2-4x+3
将-1带入有f(-1)=1+4+3=8
2、已知a、b为异面直线,AB是公垂线,直线 l //AB,则 l 与a、b的交点总数为()。
答 案:C
多选题
1、下列说法不正确的是()
- A:相切两圆的连心线经过切点
- B:长度相等的两条弧是等弧
- C:平分弦的直径垂直于弦
- D:相等的圆心角所对的弦相等
答 案:BCD
解 析:A、根据圆的轴对称性可知此命题正确,不符合题意;B、等弧指的是在同圆或等圆中,能够完全重合的弧.而此命题没有强调在同圆或等圆中,所以长度相等的两条弧,不一定能够完全重合,此命题错误,符合题意;C、此弦不能是直径,命题错误,符合题意;D、相等的圆心角指的是在同圆或等圆中,此命题错误,符合题意;故选:BCD
2、下列命题中,不正确的是()
- A:三点可确定一个圆
- B:三角形的外心是三角形三边中线的交点
- C:一个三角形有且只有一个外接圆
- D:三角形的外心必在三角形的内部或外部
答 案:ABD
解 析:A、不在同一条直线上的三点确定一个圆,故本选项错误;B.、三角形的外心是三角形三边垂直平分线的交点,所以本选项是错误;C、三角形的外接圆是三条垂直平分线的交点,有且只有一个交点,所以任意三角形一定有一个外接圆,并且只有一个外接圆,所以本选项是正确的;D、直角三角形的外心在斜边中点处,故本选项错误。故选:ABD
主观题
1、已知等差数列{an}的前n项和Sn且S5=35,S8=104.
(1)求数列{an}的通项公式;
(2)若{bn}为等比数列,b1=a2,b2=a3+2,求数列{b,}的公比q及前n项和Tn.
答 案:(1)
 所以a6=19.则数列{an}的公差
所以a6=19.则数列{an}的公差 ,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以
,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以 则
则
2、已知函数f(x)=log3(3x—1).(1)求函数f(x)的定义域;
(2)若f(x)<1,求x的取值范围.
答 案:(1)根据题意可得,3x-1>0,解得 所以函数f(x)的定义域是
所以函数f(x)的定义域是 (2)因为f(x)=log3(3x-1)<1=log33,f(x)为定义域上的增函数,所以O<3x-1<3,解得
(2)因为f(x)=log3(3x-1)<1=log33,f(x)为定义域上的增函数,所以O<3x-1<3,解得
 所以x的取值范围是
所以x的取值范围是
填空题
1、已知 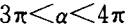 ,且α的终边与
,且α的终边与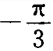 的终边互相垂直,则α=( )
的终边互相垂直,则α=( )
答 案: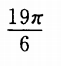
解 析:因为α的终边与-π/3的终边互相垂直
得 α=2kπ+(1/2)π-(1/3)π 或者a=2kπ-(1/2)π-(1/3)π
①若α=2kπ+(1/2)π-(1/3)π=2kπ+(1/6)π
无论k取何值,α都不在3π<α<4π之间
②若α=2kπ-(1/2)π-(1/3)π=2kπ-(5/6)π
当k=2时,α=(19/6)π,在3π<α<4π之间
2、某商品原价100元/个,现在如果打7.5折后再便宜8元,那么现在价格为_____元。
答 案:67
解 析:100×0.75-8=67元
 ,且f(1)=f(3),则f(-1)=()
,且f(1)=f(3),则f(-1)=() 
 所以a6=19.则数列{an}的公差
所以a6=19.则数列{an}的公差 ,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以
,通项公式为an=a6+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以 则
则
 所以函数f(x)的定义域是
所以函数f(x)的定义域是 (2)因为f(x)=log3(3x-1)<1=log33,f(x)为定义域上的增函数,所以O<3x-1<3,解得
(2)因为f(x)=log3(3x-1)<1=log33,f(x)为定义域上的增函数,所以O<3x-1<3,解得
 所以x的取值范围是
所以x的取值范围是
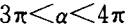 ,且α的终边与
,且α的终边与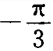 的终边互相垂直,则α=( )
的终边互相垂直,则α=( )