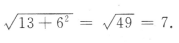单选题
1、设函数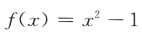 ,则f(x+1)=()
,则f(x+1)=()
答 案:B
解 析: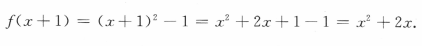
2、给出下列两个命题:①如果一条直线与一个平面垂直,则该直线与该平面内的任意一条直线垂直②以二面角的棱上任意一点为端点,在二面角的两个面内分别作射线,则这两条射线所成的角为该二面角的平面角.则()
答 案:B
解 析:一条直线与平面垂直,则直线与平面内的任意一条直线垂直,故①为真命题;二面角的两条射线必须垂直于二面角的棱,故②为假命题,因此选B选项.
3、若甲:x>1,乙: 则
则
答 案:D
解 析: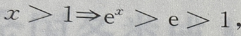 而
而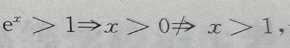 故甲是乙的充分条件,但不是必要条件
故甲是乙的充分条件,但不是必要条件
4、已知全集U=R,A={x|x≥1},B={x|-1
答 案:A
解 析:补集运算应明确知道是否包括端点.A在U中的补集是x<1, 


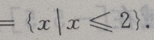
主观题
1、为了测河的宽,在岸边选定两点A和B,望对岸标记物C,测得 AB=120m,求河的宽
AB=120m,求河的宽

答 案:如图,  ∵∠C=180°-30°-75°=75°
∴△ABC为等腰三角形,则AC=AB=120m
过C做CD⊥AB,则由Rt△ACD可求得CD=
∵∠C=180°-30°-75°=75°
∴△ABC为等腰三角形,则AC=AB=120m
过C做CD⊥AB,则由Rt△ACD可求得CD= =60m,
即河宽为60m
=60m,
即河宽为60m
2、在正四棱柱ABCD-A'B'C'D'中, (Ⅰ)写出向量
(Ⅰ)写出向量 和
和 关于基底{a,b,c}的分解式;
(Ⅱ)求证:
关于基底{a,b,c}的分解式;
(Ⅱ)求证: (Ⅲ)求证:
(Ⅲ)求证:
答 案:(Ⅰ)由题意知(如图所示) 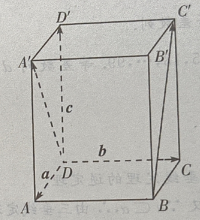
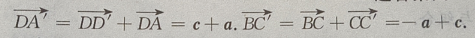
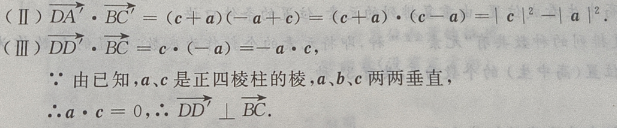
3、已知a,b,c成等差数列,a,b,c+1成等比数列.若b=6,求a和c.
答 案:由已知得 解得
解得
4、设函数f(x)= (Ⅰ)求f(x)的单调区间;
(Ⅱ)求 f(x)的极值
(Ⅰ)求f(x)的单调区间;
(Ⅱ)求 f(x)的极值
答 案:(Ⅰ)函数的定义域为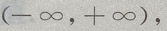
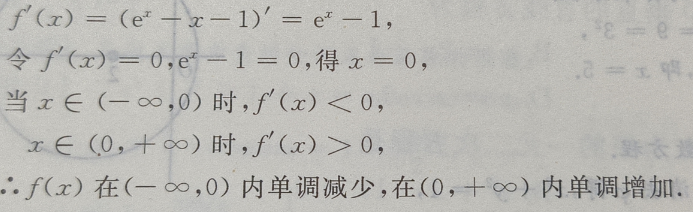 (Ⅱ)
(Ⅱ)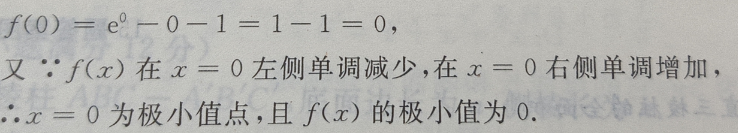
填空题
1、 的展开式是()
的展开式是()
答 案: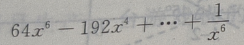
解 析: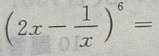
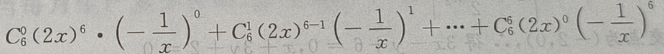

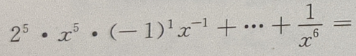
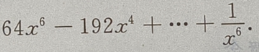
2、长方体的长、宽、高分别为2,3,6,则该长方体的对角线长为()
答 案:7
解 析:由题可知长方体的底面的对角线长为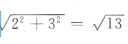 ,则在由高、底面对角线、长方体的对角线组成的三角形中,长方体的对角线长为
,则在由高、底面对角线、长方体的对角线组成的三角形中,长方体的对角线长为