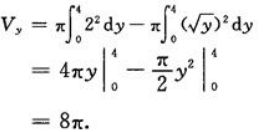判断题
1、若
，则
。（）
答 案：错
解 析：
所以
单选题
1、设函数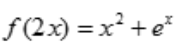
，则f'(x)＝（）.
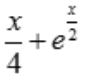
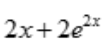
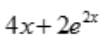
答 案：A
解 析：因为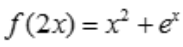
，令
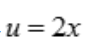，故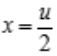
，代入原函数方程得
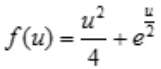，即
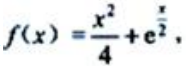所以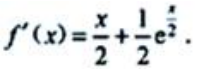
2、函数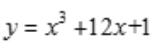
在定义域内（）.
答 案：A
解 析：函数的定义域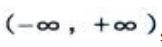为
，因为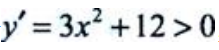
，所以y单调增加，
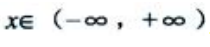.又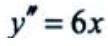
，当x＞0时，y''＞0,曲线为凹；当x＜0时，y''＜0,曲线为凸.
主观题
1、在半径为R的半圆内作一内接矩形，其中的一边在直径上，另外两个顶点在圆周上（如图所示）．当矩形的长和宽各为多少时矩形面积最大？最大值是多少？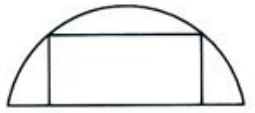
答 案：解：如图所示
，设x轴通过半圆的直径，y轴垂直且平分直径．设OA＝x，则AB＝
，矩形面积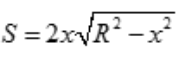
．
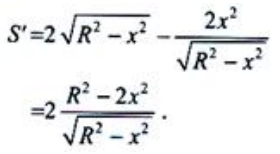令s'=0，得
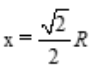（舍去负值）．
由于只有唯一驻点，根据实际问题x＝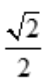
，必为所求，则AB＝
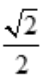R．所以，当矩形的长为
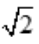R、宽为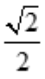
R时，矩形面积最大，且最大值S＝R2．
2、计算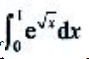
．
答 案：解：设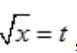
，则dx＝2tdt．当x＝0时，t＝0；当x＝1时，t＝1．则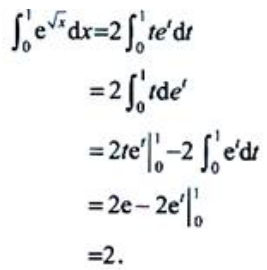
填空题
1、
＝()．
答 案：xcosx－sinx＋C
解 析：由分部积分得
2、设函数z＝ln（x＋y2），则全微分dz＝（）．
答 案：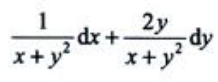
解 析：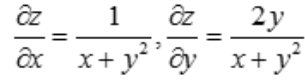
，故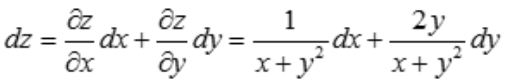
．
简答题
1、求函数
的单调区间、极值及函数曲线的凸凹性区间、拐点和渐近线.
答 案：
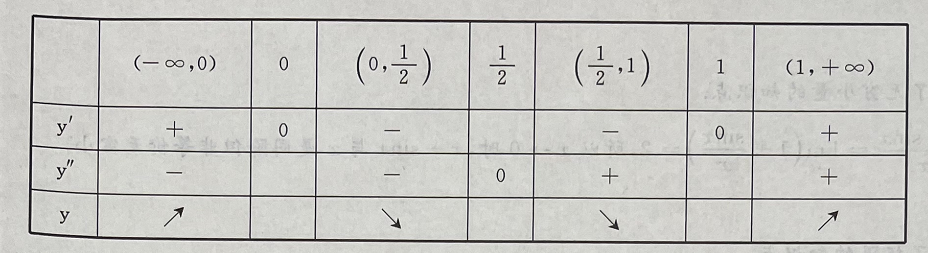所以函数y的单调增区间为
单调减区间为（0,1）；函数y的凸区间为
凹区间为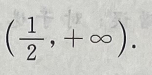
故x=0时，函数有极大值0，x=1时，函数有极小值-1，且点
为拐点，因
不存在，且
没有无意义的点，故函数没有渐近线。
2、求由曲线y＝x2与x＝2，y＝0所围成图形分别绕x轴，y轴旋转一周所生成的旋转体体积．
答 案：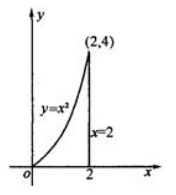
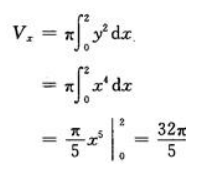绕y轴旋转一周所得的旋转体体积为
