2024年成考专升本《高等数学二》每日一练试题02月08日
精选习题
2024-02-08
11:34:06
收藏
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
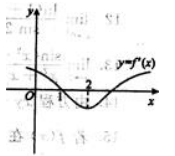
1、根据f(x)的导函数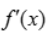 的图像(如图所示),判断下列结论正确的是( ).
的图像(如图所示),判断下列结论正确的是( ).
- A:在(∞,1)上f(x)是单调递减的
- B:在(∞,2)上f(x)是单调递减的
- C:f(1)为极大值
- D:f(1)为极小值
答 案:C
解 析:在x轴上方的曲线是表示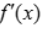 >0,而x轴下方的曲线则表示
>0,而x轴下方的曲线则表示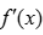 <0,注在x=1处的左边即x<1时
<0,注在x=1处的左边即x<1时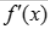 >0,而2>x>1时
>0,而2>x>1时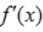 <0,根据极值的第一充分条件可知f(1)为极大值.
<0,根据极值的第一充分条件可知f(1)为极大值.
2、 ().
().
- A:
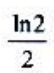
- B:0
- C:ln2
- D:-ln2
答 案:A
解 析:因为函数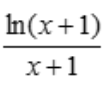 在x=1处连续,故
在x=1处连续,故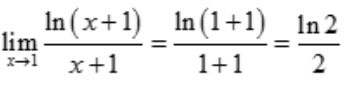 .
.
主观题
1、设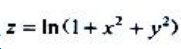 ,求dz(1,1).
,求dz(1,1).
答 案:解: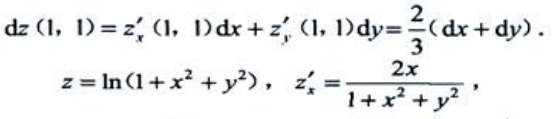
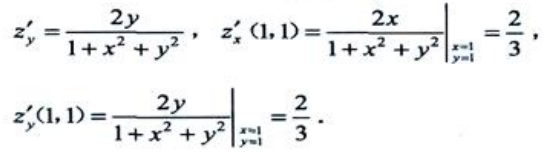
2、计算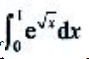 .
.
答 案:解:设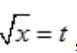 ,则dx=2tdt.当x=0时,t=0;当x=1时,t=1.则
,则dx=2tdt.当x=0时,t=0;当x=1时,t=1.则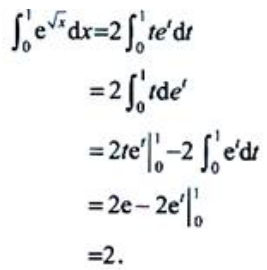
填空题
1、设函数z=x2+lny,则dz=().
答 案:2xdx+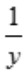 dy
dy
解 析: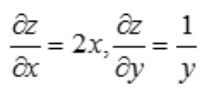 ,故
,故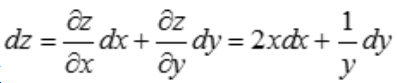 .
.
2、设函数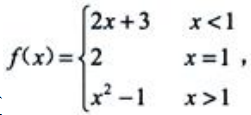 则
则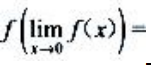 ().
().
答 案:8
解 析: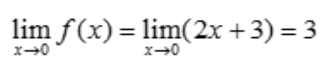 ,故
,故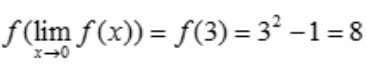 .
.
简答题
1、求函数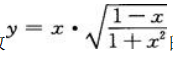 的倒数。
的倒数。
答 案:等式两边同时取对数得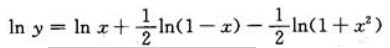 方程两边同时对x求导有
方程两边同时对x求导有 故
故
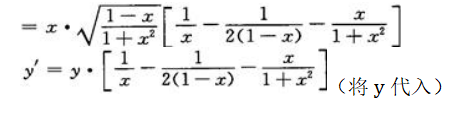
2、设函数 求常数a。使f(x)在点x=0处连续。
求常数a。使f(x)在点x=0处连续。
答 案: 要f(x)在点x=0处连续,则需
要f(x)在点x=0处连续,则需 所以a=1.
所以a=1.
更多推荐

