单选题

1、设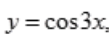则y'=（）。

• A：
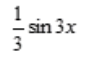
• B：
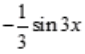
• C：
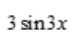
• D：

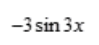
答 案：D

解 析：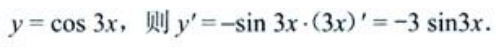

2、设y＝x＋lnx，dy＝（）。

• A：
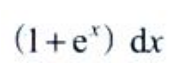
• B：
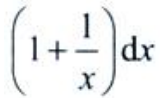
• C：
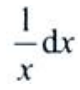
• D：

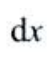
答 案：B

解 析：y＝x＋lnx，则。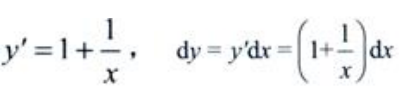

3、对于微分方程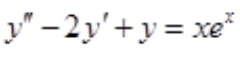，利用待定系数法求其特解y*时，下列特解设法正确的是（）。

• A：y*＝（Ax＋B）e^x
• B：y*＝x（Ax＋B）e^x
• C：y*＝Ax³e^x
• D：y*＝x²（Ax＋B）e^x

答 案：D

解 析：特征方程为r²－2r＋1＝0，特征根为r＝1（二重根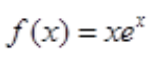），，a＝1为特征根，原方程特解为。

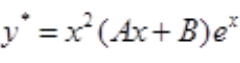主观题

1、求

答 案：解：。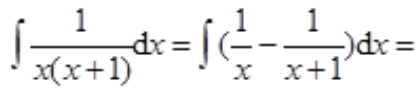

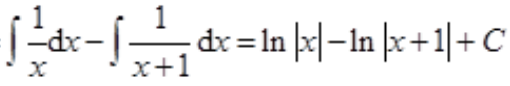
2、设f（x，y）为连续函数，交换二次积分的积分次序。

答 案：解：由题设知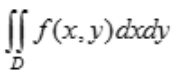中积分区域的图形应满足1≤x≤e，0≤y≤lnx，因此积分区域的图形见下图中阴影部分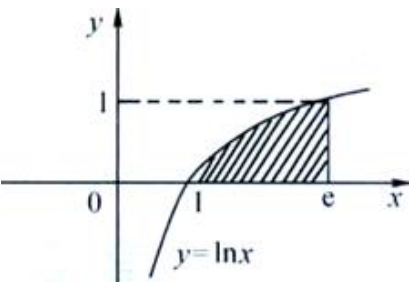．由y＝lnx，有x＝e^y。所以。

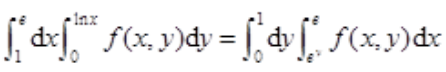3、判定级数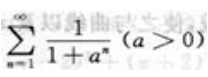的敛散性．

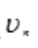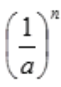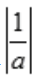答 案：解：含有参数a＞0，要分情况讨论：（1）如果0＜a＜1，则，由级数收敛的必要条件可知，原级数发散。（2）如果a＞1，令＝；因为＜1，因而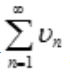是收敛的，比较法：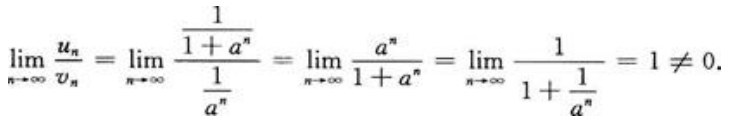
所以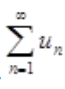也收敛。
（3）如果a＝1，则所以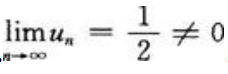，由级数收敛的必要条件可知，原级数发散。所以

填空题

1、（）。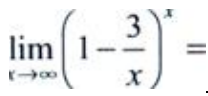

答 案：e^-3

解 析：所给极限为重要极限的形式，由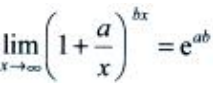，可得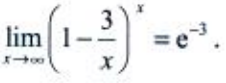

2、过原点且垂直于y轴的平面方程为（）。

答 案：y＝0

解 析：过原点且垂直于y轴的平面即x轴所在的平面，方程为y＝0。

3、（）。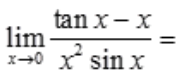

答 案：1/3

解 析：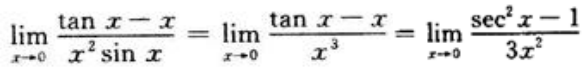

简答题

1、讨论级数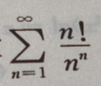敛散性。

答 案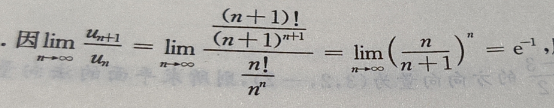：所以级数收敛。