2024年成考专升本《高等数学二》每日一练试题01月02日
精选习题
2024-01-02
11:21:55
收藏
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
1、 ().
().
- A:
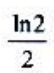
- B:0
- C:ln2
- D:-ln2
答 案:A
解 析:因为函数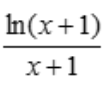 在x=1处连续,故
在x=1处连续,故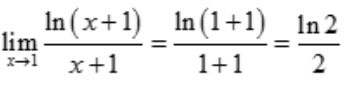 .
.
2、设 ,则dz=().
,则dz=().
- A:
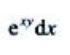
- B:
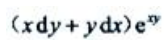
- C:
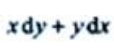
- D:
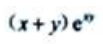
答 案:B
解 析:设u=xy,则z=eu,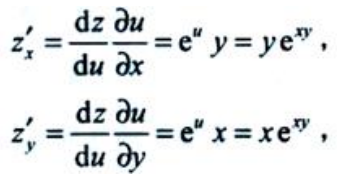
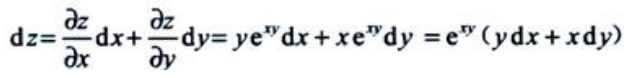 .
.
主观题
1、设函数y=esinx,求dy.
答 案:解: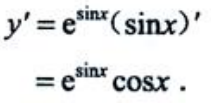 则
则
2、设函数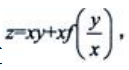 其中是f(u)二阶可微的.
其中是f(u)二阶可微的.
答 案:证明: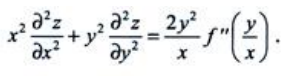 证:分别将z对x和y求偏导得
证:分别将z对x和y求偏导得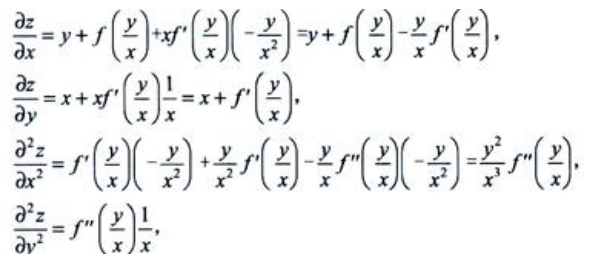 所以
所以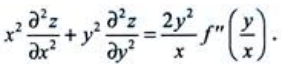
填空题
1、曲线y=x+√x在点(1,2)处的法线方程为()
答 案:2x+3y-8=0
解 析:由题可得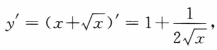 故
故 因此曲线在点(1,2)处法线的斜率是
因此曲线在点(1,2)处法线的斜率是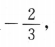 故所求法线的方程为
故所求法线的方程为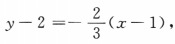 即2x+3y-8=0.
即2x+3y-8=0.
2、 =().
=().
答 案: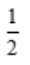
解 析: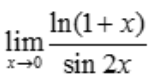 =
=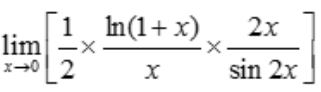 =
=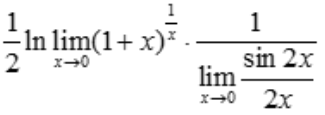 =
=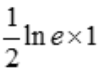 =
=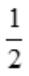 .
.
简答题
1、求曲线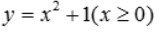 与y=x+1所围成的图形分别绕x轴和y轴旋转所得旋转体的体积.
与y=x+1所围成的图形分别绕x轴和y轴旋转所得旋转体的体积.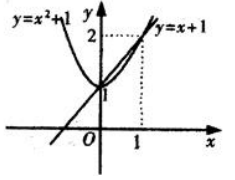
答 案:(1)绕x轴旋转的体积为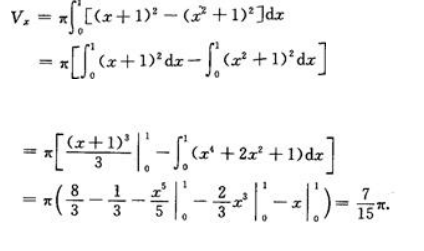 (2)绕y轴旋转的体积为
(2)绕y轴旋转的体积为
2、求函数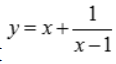 的单调区间、极值及凹凸区间.
的单调区间、极值及凹凸区间.
答 案:函数定义域为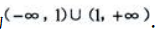 求导得
求导得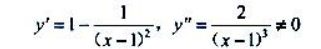 令
令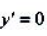 得
得 列表得
列表得 函数
函数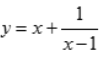 的单调增加区间为
的单调增加区间为 单调减少区间为
单调减少区间为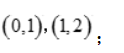
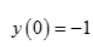 为极大值,
为极大值, 极小值;凸区间为
极小值;凸区间为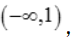 凹区间为
凹区间为 。
。
更多推荐

