单选题

1、已知向量a=(3,4),b=(0,-2),则cos=()  

• A：
• B：
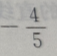
• C：
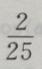
• D：

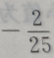
答 案：B

解 析：因为a=(3,4),b=(0,-2),  

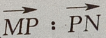2、已知点M(-2,5),N(4,2),点P在上，且=1:2，则点P的坐标为（）

• A：
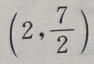
• B：(0,4)
• C：(8,2)
• D：(2,1)

答 案：B

解 析：由题意得：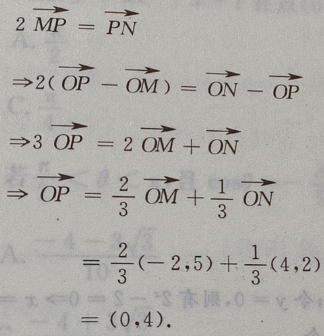  

3、设M=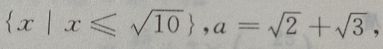那么（）

• A：
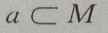
• B：
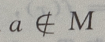
• C：
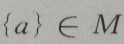
• D：

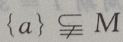
答 案：D

解 析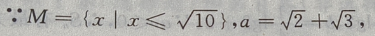： M是集合，a为元素，{a}为集合，元素与集合的关系是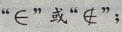集合与集合的关系是  

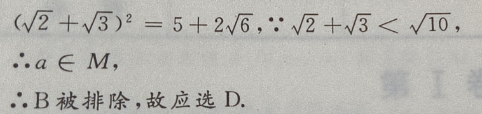
4、函数与y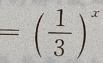的图像之间的关系是  

• A：关于原点对称
• B：关于x轴对称
• C：关于直线 y=1对称
• D：关于y轴对称

答 案：D

解 析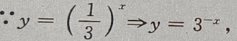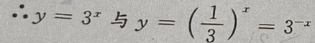：关于y轴对称，

主观题

1、已知三角形的一个内角是，面积是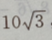周长是20,求各边的长.  

答 案：设三角形三边分别为a,b,c,∠A=60°，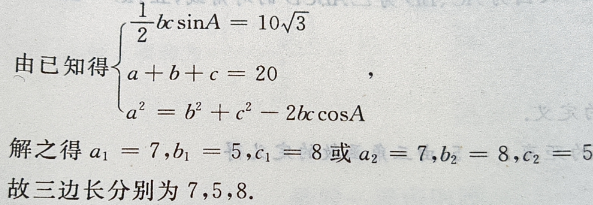  

2、已知直线l的斜率为1，l过抛物线C：的焦点，且与C交于A,B两点.
(I）求l与C的准线的交点坐标；
(II）求|AB|．

答 案：(I）C的焦点为，准线为由题意得l的方程为因此l与C的准线的交点坐标为(II）由得设A（x1,y1）.B（x2,y2），则因此

3、在△ABC中,已知三边 a、b、c 成等差数列,且最大角∠A是最小角的2倍, a: b :c.  

答 案：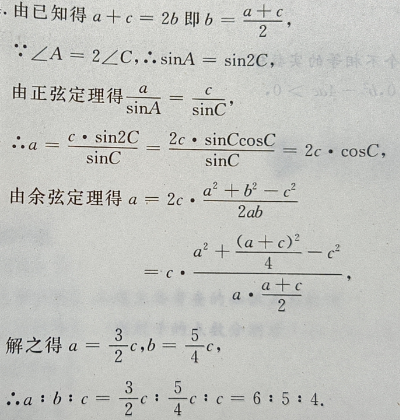

4、设函数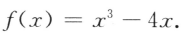
(I）求f'(2)；
(II）求f(x）在区间[一1,2]的最大值与最小值．

答 案：(I）因为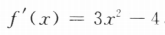，所以f'(2)=3×2²-4=8.(II）因为x＜-1，f(-1)=3.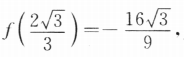f(2)=0.
所以f(x）在区间[一1,2]的最大值为3，最小值为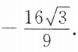

填空题

1、已知向量a=(3,2),b=(-4,x),且a⊥b，则x=（）  

答 案：6

解 析：∵a⊥b， ∴3×(-4)+2x=0 ∴x=6.  

2、函数f(x)=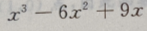在区间[-3,3]上的最大值为（）  

答 案：4

解 析：这题考的是高次函数的最值问题，可用导数来求函数在区间[-3,3]上的最值。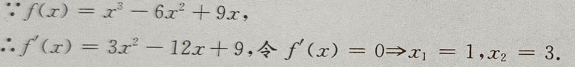 列出表格 由上表可知函数在[-3,3]上，在x=1点处有最大值为4.