单选题

1、（）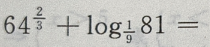  

• A：8
• B：14
• C：12
• D：10

答 案：B

解 析：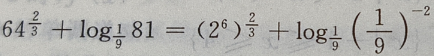

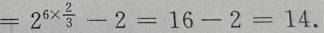
2、下列函数中，为减函数的是（）

• A：y=cosx
• B：
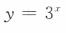
• C：
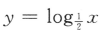
• D：

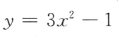
答 案：C

解 析：由对数函数的性质可知，当底数大于0小于1时，在定义域内，对数函数为减函数，故选C选项．

3、函数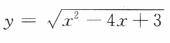的定义域是（）

• A：{x|-3≤x≤-1}
• B：{x|x≤-3或x≥-1}
• C：{x|1≤x≤3}
• D：{x|x≤1或x≥3}

答 案：D

解 析：由题可知x²-4x+3≥0，解得x≥3或x≤1，故函数的定义域为{x|x≤1或x≥3}.

4、在△ABC中，三边为a、b、c，∠B=60°，则的值是（）  

• A：大于零
• B：小于零
• C：等于零
• D：不能确定

答 案：C

解 析：由已知用余弦定理得：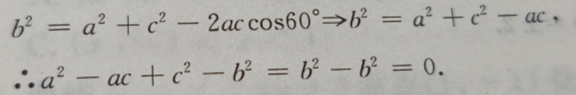  

主观题

1、在△ABC中，AB=2，BC=3,B=60°，求AC及△ABC的面积

答 案：

2、设函数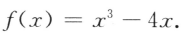
(I）求f'(2)；
(II）求f(x）在区间[一1,2]的最大值与最小值．

答 案：(I）因为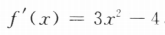，所以f'(2)=3×2²-4=8.(II）因为x＜-1，f(-1)=3.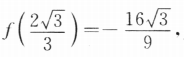f(2)=0.
所以f(x）在区间[一1,2]的最大值为3，最小值为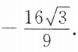

3、已知直线l的斜率为1，l过抛物线C：的焦点，且与C交于A,B两点.
(I）求l与C的准线的交点坐标；
(II）求|AB|．

答 案：(I）C的焦点为，准线为由题意得l的方程为因此l与C的准线的交点坐标为(II）由得设A（x1,y1）.B（x2,y2），则因此

4、如图：已知在△ADC中，∠C=90°，∠D=30°，∠ABC=45°，BD=20，求AC(用小数表示，保留一位小数)  

答 案：如图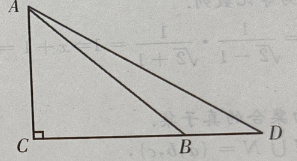  

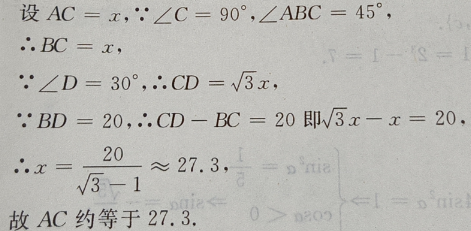
填空题

1、函数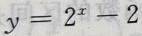的图像与坐轴的交点共有（）个  

答 案：2

解 析：当x=0，故函数与y轴交于(0,-1)点;令y=0,则有故函数与工轴交于(1,0)点,因此函数与坐标轴的交点共有2个

2、（）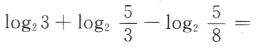

答 案：3

解 析：