单选题
1、已知直线l:3x一2y-5=0,圆C: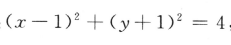 ,则C上到l的距离为1的点共有()
,则C上到l的距离为1的点共有()
- A:1个
- B:2个
- C:3个
- D:4个
答 案:D
解 析:由题可知圆的圆心为(1.-1),半径为2,圆心到直线的距离为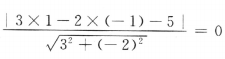 ,即直线过圆心,因此圆C上到直线的距离为1的点共有4个.
,即直线过圆心,因此圆C上到直线的距离为1的点共有4个.
2、设 成等比数列,则x等于
成等比数列,则x等于
- A:0或-2
- B:1或-1
- C:0或-2
- D:-2
答 案:C
解 析:由已知条件的得
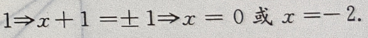
3、函数y=2sinxcosx的最小正周期是()
- A:
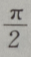
- B:

- C:
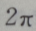
- D:

答 案:D
解 析:y=2sinxcosx=sin2x,故其最小正周期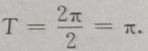
4、若函数f(x)=1+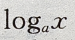 在(0,+∞)上是减函数,则()
在(0,+∞)上是减函数,则()
- A:a>1
- B:a>2
- C:1
- D:0
- D:0
答 案:D
解 析:由已知条件函数f(x)=1+ 主观题 1、在△ABC中,AB=2,BC=3,B=60°,求AC及△ABC的面积 答 案: 2、在△ABC中,已知三边 a、b、c 成等差数列,且最大角∠A是最小角的2倍, a: b :c.
答 案: 3、设函数 答 案:(I)因为 4、已知直线l的斜率为1,l过抛物线C: 答 案:(I)C的焦点为 填空题 1、函数 答 案:2 解 析:当x=0, 2、函数y= 答 案:[1,+∞) 解 析:要是函数y=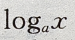 在(0,+∞)上是减函数,及对数函数
在(0,+∞)上是减函数,及对数函数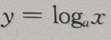 的性质可得底数0
的性质可得底数0
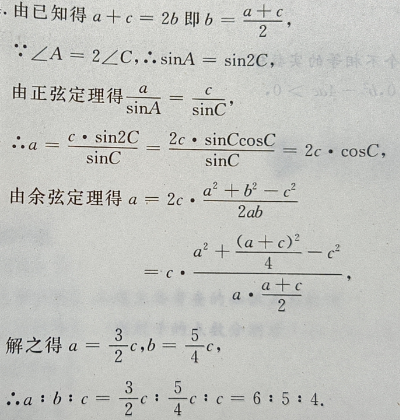
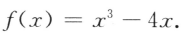
(I)求f'(2);
(II)求f(x)在区间[一1,2]的最大值与最小值.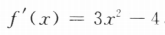 ,所以f'(2)=3×22-4=8.(II)因为x<-1,f(-1)=3.
,所以f'(2)=3×22-4=8.(II)因为x<-1,f(-1)=3.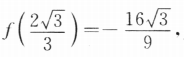 f(2)=0.
f(2)=0.
所以f(x)在区间[一1,2]的最大值为3,最小值为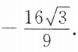
 的焦点,且与C交于A,B两点.
的焦点,且与C交于A,B两点.
(I)求l与C的准线的交点坐标;
(II)求|AB|. ,准线为
,准线为 由题意得l的方程为
由题意得l的方程为 因此l与C的准线的交点坐标为
因此l与C的准线的交点坐标为 (II)由
(II)由 得
得 设A(x1,y1).B(x2,y2),则
设A(x1,y1).B(x2,y2),则 因此
因此
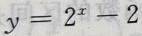 的图像与坐轴的交点共有()个
的图像与坐轴的交点共有()个
 故函数与y轴交于(0,-1)点;令y=0,则有
故函数与y轴交于(0,-1)点;令y=0,则有 故函数与工轴交于(1,0)点,因此函数
故函数与工轴交于(1,0)点,因此函数 与坐标轴的交点共有2个
与坐标轴的交点共有2个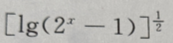 的定义域是()
的定义域是() 有意义,需使
有意义,需使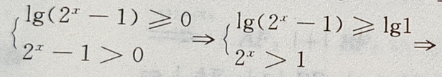
 所以函数的定义域为{x|x≥1}=[1,+∞)
所以函数的定义域为{x|x≥1}=[1,+∞)

