单选题
1、中心在坐标原点,对称轴为坐标轴,且一个顶点(3,0),虚轴长为8的双曲线方程是()
- A:
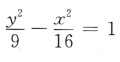
- B:

- C:

- D:

答 案:B
解 析:双曲线有一个顶点为(3,0),因此所求双曲线的实轴在x轴上,可排除A、C选项,又由于虚轴长为8,故b=4,即b2=16,故双曲线方程为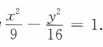
2、直线3x-4y-9=0与圆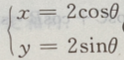 (θ为参数)的位置关系是
(θ为参数)的位置关系是
- A:相交但直线不过圆心
- B:相交但直线通过圆心
- C:相切
- D:相离
答 案:A
解 析:方法一: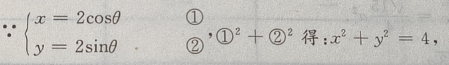 圆心O(0,0),r=2,则圆心O到直线的距离为
圆心O(0,0),r=2,则圆心O到直线的距离为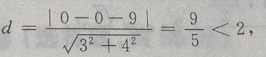 0
0
3、已知 ,则sin2α=()
,则sin2α=()
- A:
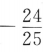
- B:
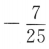
- C:
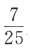
- D:
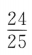
答 案:D
解 析: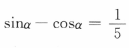 两边平方得
两边平方得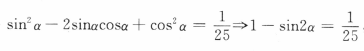 ,故
,故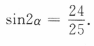
4、设0 答 案:D 解 析: 主观题 1、设函数f(x)=xlnx+x.(I)求曲线y=f(x)在点((1,f(1))处的切线方程; 答 案:(I)f(1)=1,f'(x)=2+lnx,故f'(1)=2.所以曲线y=f(x)在点(1,f(1))处的切线方程为y=2x-1.(II)令f'(x)=0,解得 2、在正四棱柱ABCD-A'B'C'D'中, 答 案:(Ⅰ)由题意知(如图所示) 3、建筑一个容积为8000 答 案: 4、在△ABC中,B=120°,BC=4,△ABC的面积为 答 案:由△ABC的面积为 填空题 1、长方体的长、宽、高分别为2,3,6,则该长方体的对角线长为() 答 案:7 解 析:由题可知长方体的底面的对角线长为 2、函数 答 案:2 解 析:当x=0时,y=



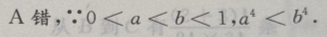
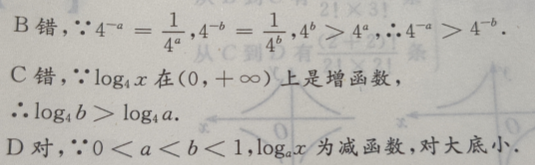
(II)求f(x)的极值. 当
当 时,f'(x)
时,f'(x) 单调递减,在区间
单调递减,在区间 单调递增.因此f(x)在
单调递增.因此f(x)在 时取得极小值
时取得极小值
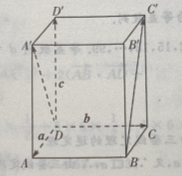
 (Ⅰ)写出向量
(Ⅰ)写出向量 关于基底{a,b,c}的分解式
(Ⅱ)求证:
关于基底{a,b,c}的分解式
(Ⅱ)求证: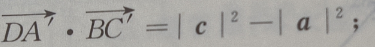 (Ⅲ)求证:
(Ⅲ)求证: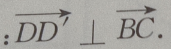
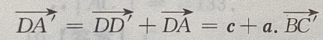
 (Ⅱ)
(Ⅱ)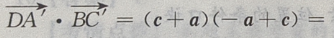
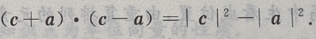 (Ⅲ)
(Ⅲ)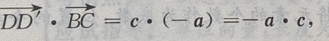 由已知,a,c是正四棱柱的棱,a,b,c两两垂直
由已知,a,c是正四棱柱的棱,a,b,c两两垂直

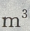 ,深为6m的长方体蓄水池,池壁每
,深为6m的长方体蓄水池,池壁每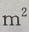 的造价为15元,池底每
的造价为15元,池底每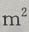 的造价为30元。(I)把总造价y(元)表示为长x(m)的函数;(Ⅱ)求函数的定义域
的造价为30元。(I)把总造价y(元)表示为长x(m)的函数;(Ⅱ)求函数的定义域
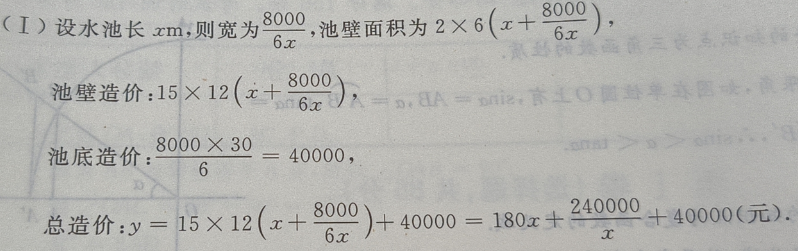

 ,求AC.
,求AC. 得
得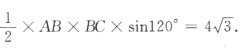 所以AB =4.因此
所以AB =4.因此 所以
所以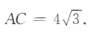
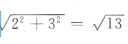 ,则在由高、底面对角线、长方体的对角线组成的三角形中,长方体的对角线长为
,则在由高、底面对角线、长方体的对角线组成的三角形中,长方体的对角线长为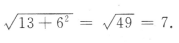
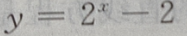 的图像与坐标轴的交点共有()
的图像与坐标轴的交点共有()
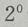 -2=-1,故函数与y轴交于(0,-1)点,令y=0,则有
-2=-1,故函数与y轴交于(0,-1)点,令y=0,则有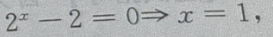 故函数与x轴交于(1,0) 点,因此函数
故函数与x轴交于(1,0) 点,因此函数 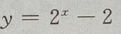 与坐标轴的交点共有 2个.
与坐标轴的交点共有 2个.

