单选题
1、下列函数中,为减函数的是()
答 案:C
解 析:由对数函数的性质可知,当底数大于0小于1时,在定义域内,对数函数为减函数,故选C选项.
2、设甲: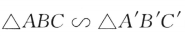 ;乙:
;乙: .则()
.则()
- A:甲是乙的必要条件但不是充分条件
- B:甲是乙的充分条件但不是必要条件
- C:甲是乙的充要条件
- D:甲既不是乙的充分条件也不是乙的必要条件
答 案:A
解 析:三角形相似不一定全等,但三角形全等一定相似,因此,甲是乙的必要条件但不是充分条件.
3、函数 与y
与y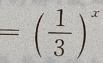 的图像之间的关系是
的图像之间的关系是
- A:关于原点对称
- B:关于x轴对称
- C:关于直线 y=1对称
- D:关于y轴对称
答 案:D
解 析: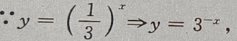
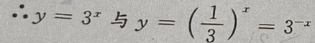 关于y轴对称,
关于y轴对称,
4、对于函数 ,有下列两个命题:①如果c=o,那么y=f(x)的图像经过坐标原点②如果a<0,那么y=f(x)的图像与x轴有公共点
,有下列两个命题:①如果c=o,那么y=f(x)的图像经过坐标原点②如果a<0,那么y=f(x)的图像与x轴有公共点
则()
- A:①②都为真命题
- B:①为真命题,②为假命题
- C:①为假命题,②为真命题
- D:①②都为假命题
答 案:B
解 析:若c=0,则函数f(x)=ax2+bx过坐标原点,故①为真命题;若a<0,而 ,则函数f(x)=ax2+bx+c的图像开口向下,与x轴没有交点,故②为假命题。因此选B选项。
,则函数f(x)=ax2+bx+c的图像开口向下,与x轴没有交点,故②为假命题。因此选B选项。
主观题
1、每亩地种果树20棵时,每棵果树收入90元,如果每亩增种一棵,每棵果树收入就下降3元,求使总收入最大的种植棵数.
答 案:设每亩增种x棵,总收入味y元,则每亩种树(20+x)棵,由题意知增种x棵后每棵收入为(60-3x) 则有y=(90-3x)(20+x)
整理得y=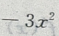 +30x+1800
配方得y=
+30x+1800
配方得y= +1875
当x=5时,y有最大值,所以每亩地最多种25棵
+1875
当x=5时,y有最大值,所以每亩地最多种25棵
2、在△ABC中,AB=2,BC=3,B=60°,求AC及△ABC的面积
答 案:
3、在△ABC中,已知三边 a、b、c 成等差数列,且最大角∠A是最小角的2倍, a: b :c.
答 案: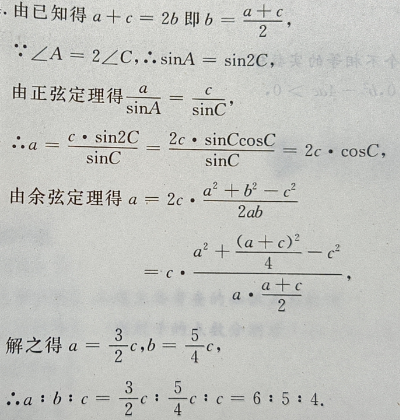
4、设函数f(x)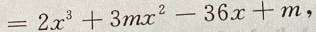 且f'(-1)=-36
(Ⅰ)求m
(Ⅱ)求f(x)的单调区间
且f'(-1)=-36
(Ⅰ)求m
(Ⅱ)求f(x)的单调区间
答 案:(Ⅰ)由已知得f'=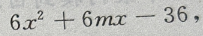 又由f'(-1)=-36得
6-6m-36=-36
故m=1.
(Ⅱ)由(Ⅰ)得f'(x)=
又由f'(-1)=-36得
6-6m-36=-36
故m=1.
(Ⅱ)由(Ⅰ)得f'(x)=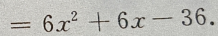 令f'(x)=0,解得
令f'(x)=0,解得 当x<-3时,f'(x)>0;
当-32时,f'(x)>0;
故f(x)的单调递减区间为(-3,2),f(x)的单调递增区间为(-∞,-3),(2,+∞)
当x<-3时,f'(x)>0;
当-32时,f'(x)>0;
故f(x)的单调递减区间为(-3,2),f(x)的单调递增区间为(-∞,-3),(2,+∞)
填空题
1、不等式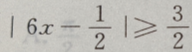 的解集是()
的解集是()
答 案: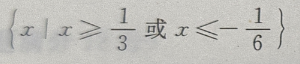
解 析: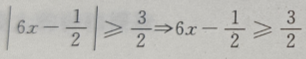 或
或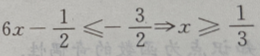 或
或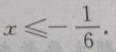
2、函数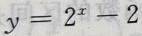 的图像与坐轴的交点共有()个
的图像与坐轴的交点共有()个
答 案:2
解 析:当x=0, 故函数与y轴交于(0,-1)点;令y=0,则有
故函数与y轴交于(0,-1)点;令y=0,则有 故函数与工轴交于(1,0)点,因此函数
故函数与工轴交于(1,0)点,因此函数 与坐标轴的交点共有2个
与坐标轴的交点共有2个
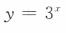
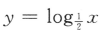
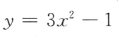
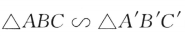 ;乙:
;乙: .则()
.则() 与y
与y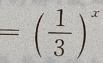 的图像之间的关系是
的图像之间的关系是
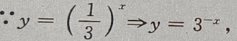
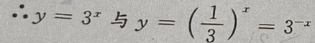 关于y轴对称,
关于y轴对称, ,有下列两个命题:①如果c=o,那么y=f(x)的图像经过坐标原点②如果a<0,那么y=f(x)的图像与x轴有公共点
,有下列两个命题:①如果c=o,那么y=f(x)的图像经过坐标原点②如果a<0,那么y=f(x)的图像与x轴有公共点 ,则函数f(x)=ax2+bx+c的图像开口向下,与x轴没有交点,故②为假命题。因此选B选项。
,则函数f(x)=ax2+bx+c的图像开口向下,与x轴没有交点,故②为假命题。因此选B选项。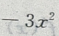 +30x+1800
配方得y=
+30x+1800
配方得y= +1875
当x=5时,y有最大值,所以每亩地最多种25棵
+1875
当x=5时,y有最大值,所以每亩地最多种25棵
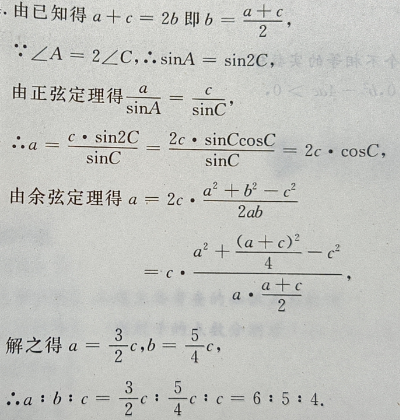
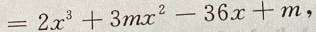 且f'(-1)=-36
(Ⅰ)求m
(Ⅱ)求f(x)的单调区间
且f'(-1)=-36
(Ⅰ)求m
(Ⅱ)求f(x)的单调区间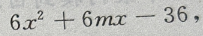 又由f'(-1)=-36得
6-6m-36=-36
故m=1.
(Ⅱ)由(Ⅰ)得f'(x)=
又由f'(-1)=-36得
6-6m-36=-36
故m=1.
(Ⅱ)由(Ⅰ)得f'(x)=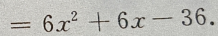 令f'(x)=0,解得
令f'(x)=0,解得 当x<-3时,f'(x)>0;
当-3
当x<-3时,f'(x)>0;
当-3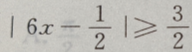 的解集是()
的解集是()
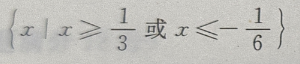
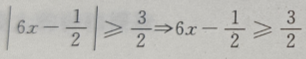 或
或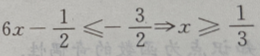 或
或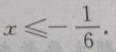
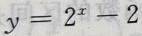 的图像与坐轴的交点共有()个
的图像与坐轴的交点共有()个
 故函数与y轴交于(0,-1)点;令y=0,则有
故函数与y轴交于(0,-1)点;令y=0,则有 故函数与工轴交于(1,0)点,因此函数
故函数与工轴交于(1,0)点,因此函数 与坐标轴的交点共有2个
与坐标轴的交点共有2个
